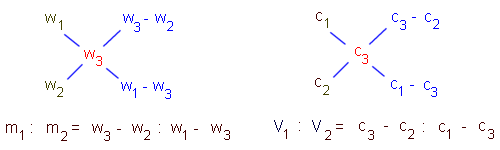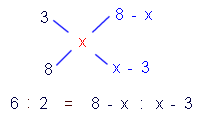A. Výklad a ukázkové příklady
Látky, které obsahují dvě nebo více složek, se nazývají směsi. Zastupení jednotlivých složek ve směsi, neboli složení soustavy
vyjadřujeme nejčastěji pomocí hmotnostního zlomku.
Hmotnostní zlomek w(A) složky A v soustavě je roven podílu hmotností m(A) složky A a soustavy m:
w(A) = m(A) / m |
{20) |
|
|
|
Příklad1: Slitina zlata stříbra, označovaná jako čtrnáctikarátové zlato, obsahuje ve 24 hmotnostních
dílech slitiny 14 dílů čistého zlata, Jaký je hmotnostní zlomek zlata ve slitině?
| = |
Podle (20) platí:
w(Au) = m(Au)/m(slitina) = 14 / 24 = 0,583 = 58,3 %
Výsledek: Hmotnostní zlomek zlata ve čtrnáctikarátovém zlatu je 58,3 %.
|
Příklad2: Mořské řasy obsahují 0,03 % jodu. Jaká by byla hmotnost jodu získaná z 5 tuny mořských řas?.
| = |
Protože je hmotnostní zlomek jodu v řasách 0,03 %, platí:
 |
100 t řas . . . . . . . 0,03 t jodu
5 t řas . . . . . . . . . . x t jodu
|  |
x : 0,03 = 5 : 100
x = 5 . 0,03 / 100 = 0,0015 t = 1,5 kg
Výsledek: Z 5 t mořských řas lze získat 1,5 kg jodu.
|
Roztok je homogenní směs složená ze dvou (nebo několika) látek. Zastoupení jednotlivých složek
v roztoku označujeme jako koncentrace roztoku.
Koncentraci roztoku udává nejčastěji:
1. Hmotnostní zlomek (hmotnostní procentová koncentrace)
2. Objemový zlomek (objemová procentní koncentrace)
3. Hmotnostní koncentrace
4. Molární koncentrace
5. Normální koncentrace
Hmotnostní zlomek w(A) rozpuštěné látky A v roztoku je podíl hmotnosti m(A) rozpuštěné
látky A a hmotnosti m roztoku.
w(A) = m(A) / m
Vyjadřuje se nejčastěji v procentech a udává tedy počet gramů rozpuštěné látky ve 100 g roztoku
|
{21) |
|
Příklad 3: Roztok jsme získali rozpuštěním 30 g chloridu sodného ve 100 g vody.
Vypočtěte hmotnostní zlomek NaCl v roztoku.
| = |
Hmotnost roztoku je 30 + 100 = 130 g a dosadíme do (21):
w(NaCl) = 30 / 130 = 0,2308 = 23,08 %
Výsledek: Získali jsme 23,08 % roztok chloridu sodného.
|
Příklad 4: Do prázdného šálku jsme nalili 200 g kávy a přisypali 3 sáčky porcovaného cukru
(po 5 g). Určete hmotnostní zlomek cukru v takto připravené kávě.
| = |
Hmotnost roztoku je 200 + 15 = 215 g.
Zajímá nás hmotnostní zlomek = počet gramů cukru rozpuštěného ve 100 g roztoku (21).
Tentokrát zkusíme trojčlenku:
 |
215 g (oslazené) kávy . . . . . . . 15 g cukru
100 g (oslazené) kávy . . . . . . . x g cukru
|  |
x : 15 = 100 : 215
x = 100 . 15 / 215 = 6,98 g = 6,98 %
Výsledek: Hmotnostní zlomek rozpuštěného cukru v kávě je 6,98 %.
|
Příklad 5: Kolik gramů hydroxidu sodného je zapotřebí k přípravě 700 ml 25 % roztoku,
jehož hustota je 1,277 g.cm-3?
| = |
Objem výsledného roztoku má být: V = 700 ml = 700 cm3
Hmotnost výsledného roztoku má být: m = V.r = 700 . 1,277 = 893,9 g
Roztok má mít hmotnostní zlomek 25 % tedy platí:
 |
100 g roztoku . . . . . . . . 25 g NaOH
893,9 g roztoku . . . . . . . . . x g NaOH
|  |
x : 25 = 893,9 : 100
x = 893,9 . 25 / 100 = 223,48 g NaOH
Výsledek: Na přípravu 700 ml 25 % roztoku je třeba 223,5 g hydroxidu sodného.
|
Objemový zlomek f(A) rozpuštěné látky A v roztoku je podíl objemu V(A) rozpuštěné
látky A a objemu V roztoku.
f(A) = V(A) / V
Vyjadřuje se nejčastěji v procentech a udává tedy počet dm3 rozpuštěné látky ve 100 dm3 roztoku
|
{22) |
|
Příklad 6: Objemový zlomek kyslíku ve vzduchu je 21,9 %. Vypočtěte, jaký objem zaujímá
kyslík v místnosti o rozměrech 5 x 4 x 2,5 m naplněné vzduchem.
| = |
Objem místnosti je 5.4.2,5 = 50 m 3.
Objemový zlomek kyslíku je 21,9 %, tedy ve 100 dm3 vzduchu je 21,9 dm3 kyslíku.
 |
100 dm3 vzduchu . . . . . . . 21,9 dm3 kyslíku
50 000 dm3 vzduchu . . . . . . . . . x dm3 kyslíku
|  |
x : 21,9 = 50000 : 100
x = 50000 . 21,9 / 100 = 10950 dm3 = 10,95 m3
Výsledek: Kyslík v místnosti zaujímá objem přibližně 11 m3.
|
Hmotnostní koncentrace cm(A) rozpuštěné látky A v roztoku je podíl hmotnosti m(A) rozpuštěné
látky A a objemu V roztoku.
cm(A) = m(A) / V
Vyjadřuje se nejčastěji v g.dm-3
|
{23) |
|
Příklad 7: Odpařením 12,0 cm3 vodného roztoku NaCl se získalo 0,132 g NaCl.
Vypočtěte hmotnostní koncentraci NaCl v tomto roztoku..
| = |
cm(NaCl) = m(NaCl) / V = 0,132 / 12 = 0,011 g.cm-3
Výsledek: Hmotnostní koncentrace NaCl v roztoku byla 0,011 g.cm-3.
|
Molární koncentrace (látková koncentrace) c(A) rozpuštěné látky A v roztoku je podíl látkového množství n(A) rozpuštěné
látky A a objemu V roztoku.
cm(A) = n(A) / V
Vyjadřuje se nejčastěji v mol.dm-3
Molární koncentrace tedy udává počet molů látky v jednom dm3 roztoku.
O roztok, který má molární koncentraci 2 mol.dm-3 říkáme, že je 2molární a označujeme jako 2M roztok.
| {24)
|
|
Příklad 8: Vypočtěte molární koncentraci roztoku NaOH,
který vznikl rozpuštěním 10 g NaOH v 125 cm3 vody.
| = |
Vypočteme nejprve látkové množství rozpuštěného NaOH:
n(NaOH) = m(NaOH) / Mr(NaOH) = 10 / 40 = 0,25 mol
Nyní dosadíme do vztahu (24):
c(NaOH) = n(NaOH) / V = 0,25 / 0,125 = 2 mol.dm-3
Výsledek: Molární koncentrace NaOH v roztoku je 2 mol.dm-3.
|
Příklad 9: Vypočtěte, kolik gramů dusitanu draselného
potřebujeme na přípravu 400 cm3 4M roztoku dusitanu draselného.
| = |
Hmotnost 1 molu KNO2 je 85,11 g, hmotnost 4 molů KNO2 je tedy 4.85,11 = 340,44 g
Toto množství bychom museli rozpustit v 1 dm3, aby byl 4molární.
Trojčlenkou zjistíme, kolik musíme rozpustit ve 400 cm3:
 |
1000 cm3 . . . . . . . 340,44 g KNO2
400 cm3 . . . . . . . . . . . . . x g KNO2
|  |
x : 340,44 = 400 : 1000
x = 400 . 340,44 / 1000 = 10950 dm3 = 136,18 g KNO2
Výsledek: Na přípravu 400 cm3 4M roztoku dusitanu draselného potřebujeme
136,18 g KNO2.
|
Chemický ekvivalent látky je část molekuly (atomu, iontu), která je při dané reakci chemicky
ekvivalentní jednomu atomu vodíku (iontu H+, elektronu).
1 mol chemických ekvivalentů nazýváme val .
Při dané reakci reaguje vždy 1 val jedné látky s 1 valem jiné látky.
Valová hmotnost Mv - hmotnost 1 valu látky - je podílem hmotnosti Mr
1 molu a valence v (sytnost kyseliny, zásady):
Mv = Mr / v
tedy
1 val = 1 mol / v
|
{25) |
Valové množství nv látky je podílem hmotnosti m látky a valové hmotnosti látky Mv:
nv = m / Mv
|
{26) |
|
Příklad 10: Vypočtěte valovou hmotnost uhlíku v oxidu uhličitém.
| = |
Uhlík v oxidu uhličitém má valenci 4 a podle (25) platí:
Mv = Mr / 4 = 12 / 4 = 3 g
Výsledek: Hmotnost 1 valu uhlíku v oxidu uhličitém je 3 g.
|
Příklad 11: Při hoření hliníku na oxid hlinitý se spotřebovalo 5 g hliníku.
Vypočítejte valové množství hliníku.
| = |
Hliník má v oxidu hlinitém valenci 3 a pro valovou hmotnost hliníku platí:
Mv = Mr / 3 = 26,98 / 3 = 8,99 g
Valové množství hliníku vypočteme podle vztahu (26):
nv = m / Mv = 5 / 8,99 = 0,556 val
Výsledek: Valové množství hliníku je 0,556 val.
|
Příklad 12: Vypočítejte valovou hmotnost kyseliny sírové.
| = |
H2SO4 je dvojsyrná kyselina, platí tedy podle (25):
Mv = Mr / 2 = 98,08 / 2 = 49,04 g.val-1
Výsledek: Valové hmotnost H2SO4 je 49,04 g.val-1.
|
Příklad 13: Kolik gramů hydroxidu železitého představuje hmotnost 1 valu?
| = |
Fe(OH)3 je trojsyrná zásada, platí tedy podle (25):
Mv = Mr / 3 = 106,87 / 3 = 35,6 g
Výsledek: Valové hmotnost 1 valu Fe(OH)3 je 35,6 g.
|
Normální koncentrace cn(A) rozpuštěné látky A v roztoku je podíl valového
množství nv(A) látky A a objemu V roztoku.
cn(A) = nv(A) / V
Vyjadřuje se nejčastěji v val.dm-3
Normální koncentrace tedy udává počet valů látky v jednom dm3 roztoku.
O roztok, který má normální koncentraci 2 val.dm-3 říkáme, že je 2normální a označujeme jako 2N roztok.
| {27)
|
|
Příklad 14: Kolik gramů chloridu sodného potřebujeme navážit k přípravě
2 litrů 0,1N vodného roztoku?
| = |
Hmotnost jednoho molu NaCl je 58,44 g.
Hmotnost jednoho valu NaCl je 58,44 / 1 = 58,44 g.
Na 1 dm3 1N roztoku NaCl bychom potřebovali 58,44 g NaCl.
Na 1 dm3 0,1N roztoku NaCl bychom potřebovali 1/10 valu NaCl, tedy 5,844 g NaCl.
Na 2 litry = 2 dm3 dvakrát tolik, tj. 2.5,844 = 11,688 g NaCl.
Výsledek: Na přípravu 2 litrů 0,1N roztoku NaCl potřebujeme 11,69 g NaCl.
|
Příklad 15: Kolik gramů hydroxidu vápenatého je ve 100 cm3 0,2N roztoku Ca(OH)2?
| = |
Hmotnost 1 molu Ca(OH)2 je 74,1 g , 1 val má hmotnost 74,1 / 2 = 37,05 g
1 dm3 1N roztoku Ca(OH)2 obsahuje 37,05 g.
1 dm3 0,1N roztoku Ca(OH)2 obsahuje 3,705 g.
1 dm3 0,2N roztoku Ca(OH)2 obsahuje 2.3,705 = 7,41 g.
100 cm3 0,2N roztoku Ca(OH)2 obsahuje desetkrát méně, tedy 0,741 g Ca(OH)2.
Výsledek: Ve 100 cm3 0,2N roztoku je 0,741 g Ca(OH)2.
|
Příklad 16: Vypočtěte normální koncentraci 30% HCl o hustotě 1,15 g.cm-3
pro 100 g roztoku.
| = |
HCl je jednosytná kyselina, proto valové množství je rovno látkovému množství a normalita = molarita.
Hmotnost HCl v 100 g roztoku je 30 g ( w(HCl) = 30% ) a látkové množství HCl:
n(HCl) = m(HCl) / Mr(HCl) = 30 / 36,46 = 0,8228 mol
Objem roztoku vypočteme pomocí hustoty:
V = m / r = 100 / 1,15 = 86,9565 cm3 = 0,0869565 dm3
Molární (normální) koncentrace roztoku HCl tedy je:
cn = 0,8228 / 0,0869565 = 9,46 val.dm-3
Výsledek: Roztok HCl má normální koncentraci 9,46 val.dm-3 (9,46N roztok HCl).
|
Ředění a směšování roztoků Při řešení těchto příkladů používáme nejčastěji metod:
1. Směšovací rovnice
2. Křížové pravidlo
3. Úvaha, trojčlenka
Směšovací rovnice s hmotnostními zlomky
Smísíme-li roztoky o hmotnostech m1, m2 s hmotnostními
zlomky w1, w2, vznikne roztok s hmot.zlomkem w3, pro který platí:
m1.w1 + m2.w2 = (m1 + m2).w3
|
{28) |
Směšovací rovnice s látkovými koncetracemi
Smísíme-li roztoky o objemech V1, V2 s látkovými koncentracemi
c1, c2, vznikne roztok s látkovou koncentrací c3, pro který platí:
V1.c1 + V2.c2 = (V1 + V2).c3
|
{29) |
|
Příklad 17: Vypočtěte koncentraci roztoku chloridu sodného, který vznikne smísením
6 dm3 3M roztoku NaCl a 2 dm3 8M roztoku NaCl.
| = |
Dosadíme do směšovací rovnice (29):
6.3 + 2.8 = (6 + 2).c3 a dostáváme:
c3 = 34 / 8 = 4,25 M
Výsledek: Vznikne 4,25M roztok NaCl.
|
Křížové pravidlo vznikne ze směšovacích rovnic a udává mechanický způsob výpočtu.
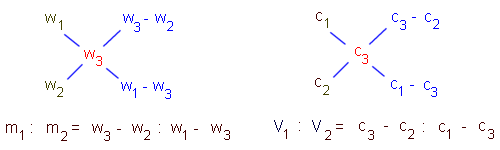
| {29) |
|
Příklad 18: Předchozí příklad vyřešíme užitím křřžového pravidla.
| = |
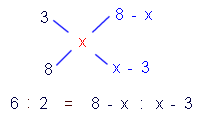
Odsud dostáváme:
3.(x - 3) = 8 - x
4x = 17
x = 4,25
Výsledek: Vznikne 4,25M roztok NaCl.
|
Příklad 19: Předchozí příklad vyřešíme úvahou.
| = |
Celkový objem roztoku bude 2 + 6 = 8 dm3
Celkové látkové množství (n = c . V) bude: 6.3 + 2.8 = 34 mol
Výsledná koncentrace (c = n / V) tedy je: c = 3 / 8 = 4,25 mol.dm-3
Výsledek: Vznikne 4,25M roztok NaCl.
|
Pro přidávání (odebírání) rozpouštědla je hmotnostní zlomek (koncentrace) rozpouštědla w2 = 0 (c2 = 0).
Pozor, při odebírání (odpařování,zreagování) se hmotnost (objem) odečítá, tedy:
Odebírání rozpoštědla
m1.w1 = (m1 - m2).w3
V1.c1 = (V1 - V2).c3
|
{30) |
Pro přidávání (odebírání) čisté (rozpouštěné) látky je hmotnostní zlomek čisté látky w2 = 1.
Pozor, při odebírání (odpařování,zreagování) se hmotnost (objem) odečítá, tedy:
Odebírání čisté (rozpuštěné) látky
m1.w1 - m2 = (m1 - m2).w3
Tedy: V1.c1 - V2.c2 = (V1 + V2).c3
Pokud se přidáním čisté látky objem nezmění ( V1 + V2 = V1) a koncentrace je látková ( V2.c2 =
V2.n2 / V2 = n2) dostáváme:
V1.c1 - n2 = V1.c3
|
{31) |
|
Příklad 20: Vypočtěte objem koncentrované kyseliny sírové (w1=98%,
r1 = 1,836 g.cm-3) potřebného k přípravě 3 dm3 roztoku této kyseliny
pro plnění akumulátoru (w3=32%, r3 = 1,235 g.cm-3)
| = |
Vypočteme nejprve hmotnosti příslušných roztoků:
koncentrovaná kyselina: m1 = V1.1,836
voda pro ředění: m2 = (3 - V1).1
kyselina pro plnění: m3 = 3.1,235 = m1 + m2
Dosadíme do směšovací rovnice (voda má w2=0) (28):
1,836V . 0,98 + 1.(3 - V).0 = 3.1,235.0,32
Po úpravách dostáváme:
V = 3.1,235.0,32/1,836.0,98 = 0,65893 dm3 = 658,9 cm3
Výsledek: Na přípravu 3 litrů akumulátorové kyseliny je třeba 658,9 ml koncentované kyseliny sírové.
|
B. Příklady s krokovou kontrolou e-učitele
C. Příklady na procvičení učiva
Na následujících příkladech s výsledky se můžete zdokonalit ve znalostech učiva této lekce.
Pokud si nevíte s příkladem rady, užijte stručné nápovědy - Help.
| Příklady označené | A mají největší obtížnost, | B střední a | C nejmenší. |
D. Kontrolní test
E. Hodnocení výsledků a komunikace s učitelem (tutorem)
Vytisknout certifikat
Hodnocení výsledků:
Komunikace s učitelem (tutorem):
Tato část je určena pouze pro registrované uživatele. Zaregistrujte se!
|