A. Výklad a ukázkové příklady
Derivace funkce má široké uplatnění nejen v matematice, ale i ve fyzice, chemii i ostatních přírodních vědách.
Pokud známe funkci, charakterizující určitý děj, potom derivace této funkce popisuje okamžitou změnu tohoto děje, tedy
okamžitou rychlost děje. To je hlavní motiv řady příkladů, z nichž některé si ukážeme. Rozdělíme je do několika oblastí:
Tečna a normála grafu funkce
Touto aplikací derivace jsme se již zabývali v 3.lekci, proto jenom stručně shrneme. Derivace funkce udává směrnici tečny kt ke grafu funkce f v bodě T[xo,yo].
Rovnice tečny grafu funkce v bodě T[xo,yo] má tvar:
y - yo = kt(x - xo)
Normála je přímka procházející bodem T kolmo k tečně, její směrnice kn = -1/kt a rovnice:
y - yo = kn(x - xo)
Příklady najdete ve zmiňované 3.lekci.
Nalezení největší (nejmenší) hodnoty
V úlohách typu najděte nejkratší vzdálenost, největší objem, maximální rychlost atd. aplikujeme hledání
globálních (lokálních) extrémů na funkci, popisující aktuální veličinu.
Příklad 40:
Vypočtěte rozměry co největšího (plochou) obdélníkového výběhu pro slepice, máme-li na oplocení k dispozici 50 m pletiva a jednu stranu
výběhu tvoří stěna budovy.
| = |
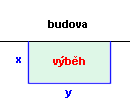 Označme šířku obdélníkového výběhu x a délku y metrů (podle obrázku).
Vzhledem k délce pletiva platí: 2x + y = 50
Označme šířku obdélníkového výběhu x a délku y metrů (podle obrázku).
Vzhledem k délce pletiva platí: 2x + y = 50
tedy y = 50 - 2x kde x 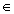 (0,25) (0,25)
Pro obsah výběhu platí: S = x.y = x.(50 - 2x)
Obsah výběhu je funkcí jeho šířky x.
Máme určit, kdy je obsah největší, tedy hledáme globální maximum funkce f:
S = x.y = x.(50 - 2x) = 50x - 2x2 pro x 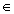 (0,25). (0,25).
Derivace S' = 50 - 4x je zde spojitá a jediným stacionárním bodem je x = 12,5.
Vlevo od tohoto bodu je derivace kladná (např. S´(10) = 10) , vpravo záporná (např. S´(20) = -30),
proto v bodě x = 12,5 nastává lokální maximum pro hodnotu S. Protože je to jediný extrém, je to i globální extrém -
největší hodnota funkce.
Délka výběhu potom bude y = 50 - 2.12,5 = 25 m.
Výsledek: Výběh má největší obsah pro délku 25 m a šířku 12,5 m.
|
Obecně tedy musíme nejprve určit funkci popisující zkoumanou závislost a splňující dané podmíny.
(V našem příkladě funkci vyjadřující obsah výběhu při dané délce pletiva)
Požadovaná funkce musí mít pouze jednu proměnnou - jen u funkcí jedné proměnné dokážeme zatím zjišťovat jejich průběh a další vlastnosti.
Potom u této funkce hledáme globální extrémy.
Příklad 41:
Na válcovou konzervu se má spotřebovat 5 dm2 bílého plechu. Jaké má mít konzerva rozměry, aby měla
přitom největší objem?
| = |
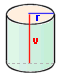 Označme poloměr podstavy válcové konzervy r a její výšku v podle obrázku.
Označme poloměr podstavy válcové konzervy r a její výšku v podle obrázku.
Objem této konzervy určuje funkce f: V = p.r2.v
U této funkce nás podle zadání zajímá globální maximum.
Má to ale háček. Jednak je to funkce dvou proměnných r, v (její průběh zatím neumíme prozkoumat) a
druhak funkce nesplňuje podmínku ohledně spotřeby plechu.
Spotřeba plechu na konzervu je dána jejím povrchem: S = 2.p.r2 +
2.p.r.v
Musí platit: 5 = 2.p.r2 + 2.p.r.v
Výška konzervy v (ta se bude vyjadřovat snadněji) musí splňovat podmínku:
5 - 2.p.r2 = 2.p.r.v
Tedy: v = (5 - 2.p.r)/(2.p.r)
Dosadíme za v do funkce pro objem: V = p.r2.r.(5 - 2.p.r)/2 =
2,5.r - p.r3
a tím jsme našli požadovanou funkci jedné proměnné splňující zadané podmínky.
Nyní budeme hledat její globální maximum. První derivace: V´ = 2,5 - 3.p.r2
má nulový bod 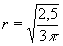 (druhý, opačný nemá pro nás význam).
Vlevo od něho (je to přibližně 0,515) je derivace kladná (V´(0) = 2,5 > 0) a vpravo je záporné (V´(1) = 2,5 - 3.p < 0).
Proto v tomto bodě nastává lokální maximum. Protože je to v intervalu (0,+ (druhý, opačný nemá pro nás význam).
Vlevo od něho (je to přibližně 0,515) je derivace kladná (V´(0) = 2,5 > 0) a vpravo je záporné (V´(1) = 2,5 - 3.p < 0).
Proto v tomto bodě nastává lokální maximum. Protože je to v intervalu (0,+ ) jediný
extrém, je zároveň i globální maximum této funkce. Poloměr požadované konzervy je tedy přesně ) jediný
extrém, je zároveň i globální maximum této funkce. Poloměr požadované konzervy je tedy přesně 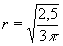 , zaokrouhleně r = 0,515 dm.
, zaokrouhleně r = 0,515 dm.
Zbývá dopočítat výšku konzervy: 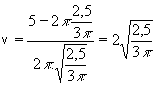 (což je přibližně 1,03 dm). (což je přibližně 1,03 dm).
Výsledek: Maximální objem má konzerva pro poloměr přibližně 5,15 cm a výšku přibližně 10,3 cm.
|
A něco z fyziky.
Příklad 42:
Výkon baterie s elektromotorickým napětím Ue a vnitřním odporem Ri je
P = UeI - I2Ri. Při jakém proudu bude výkon maximální?
| = |
Vzhledem k otázce považujeme vztah P = UeI - I2Ri
za funkci vyjadřující závislost výkonu P na proměnné I (Ue, Ri jsou konstatnty)
a budeme hledat její maximum.
Derivace P podle I je: PI´ = Ue - 2.I.Ri
Stacionární body získáme řešením rovnice: Ue - 2.I.Ri = 0 s neznámou I.
Stacionární bodem je: I = Ue/2.RI.
Vlevo od tohoto bodu (např. pro Ue/4.RI) je 1.derivace kladná
(PI´(Ue/4.RI) = Ue - 2.(Ue/4.RI).Ri =
Ue/2 > 0)
Vpravo od tohoto bodu (např. pro Ue/.RI) je 1.derivace záporná
(PI´(Ue/RI) = Ue - 2.(Ue/RI).Ri =
Ue - 2.Ue = -Ue < 0)
Pro I = Ue/2.RI nabývá tedy P maxima.
Výsledek: Maximálního výkonu baterie dosahuje při proudu I = Ue/2.RI .
|
l´Hospitalovo pravidlo
Při výpočtu limit nám dělal problémy neurčitý výraz typu 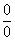 ,
tedy ,
tedy 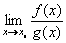 , kde f(xo) = g(xo) = 0. Zkusme se na tento
případ podívat jinak - "derivačně". Vyjádřeme limitu podílu derivací funkcí ve zmíněném bodě xo: , kde f(xo) = g(xo) = 0. Zkusme se na tento
případ podívat jinak - "derivačně". Vyjádřeme limitu podílu derivací funkcí ve zmíněném bodě xo:
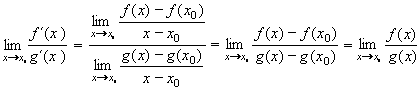 , protože g(xo) = f(xo) = 0 , protože g(xo) = f(xo) = 0
Tím dostáváme první l´Hospitalovo pravidlo, které umožňuje z existence limity podílu derivovaných funkcí vypočítat limitu podílu funkcí
u tohoto neurčitého výrazu
:
první l´Hospitalovo pravidlo:
Máme-li vypočítat limitu 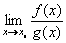 , neurčitého výrazu typu , neurčitého výrazu typu
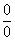 a jsou-li derivace f´(x), g´(x) spojité v bodě xo, g´(xo)
a jsou-li derivace f´(x), g´(x) spojité v bodě xo, g´(xo) 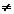 0 a existuje limita 0 a existuje limita
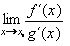 , pak je to i hledaná limita, tedy platí: , pak je to i hledaná limita, tedy platí:
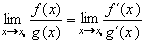
| (39) |
|
Příklad 43:
Vypočtěte: 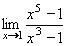
| = |
Jedná se o neurčitý výraz typu 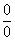 . .
Vypočteme derivaci čitatele a derivaci jmenovatele:
f´(x) = 5.x4
g´(x) = 3.x2
Obě derivace jsou v každém bodě (tedy i v bodě x = 1) spojité a g´(1) = 3 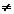 0.
Múžeme tedy l´Hospitalovým pravidlem vypočítat limitu pomocí derivací: 0.
Múžeme tedy l´Hospitalovým pravidlem vypočítat limitu pomocí derivací:
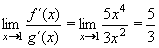 a to je i výsledná, hledaná limita. a to je i výsledná, hledaná limita.
Výsledek: 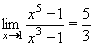
|
l´Hospitalovo pravidlo lze aplikovat i opakovaně:
Příklad 44:
Vypočtěte: 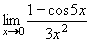
| = |
Jedná se o neurčitý výraz typu 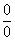
Vypočteme derivaci čitatele a derivaci jmenovatele:
f´(x) = 5.sin5x
g´(x) = 6x
Po aplikaci l´Hospitalova pravidla: 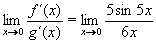 dostáváme opět neurčitý výraz typu
dostáváme opět neurčitý výraz typu 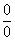
Vypočteme opět derivaci čitatele a derivaci jmenovatele:
f´(x) = 25.cos5x
g´(x) = 6
Tentokrát již požadovaná limita derivovaných funkcí existuje:
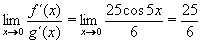 a tím dostáváme i výslednou, hledanou limitu. a tím dostáváme i výslednou, hledanou limitu.
Výsledek: 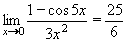
|
Obdobným způsobem lze na výpočet limity 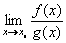 typu typu 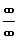 aplikovat druhé l'Hospitalovo pravidlo.
:
aplikovat druhé l'Hospitalovo pravidlo.
:
druhé l´Hospitalovo pravidlo:
Máme-li vypočítat limitu 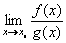 , neurčitého výrazu typu , neurčitého výrazu typu
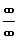 a existuje limita
a existuje limita 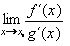 , pak je to i hledaná limita, tedy platí: , pak je to i hledaná limita, tedy platí:
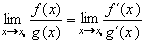 . Pravidlo platí i pro limity v nevlastních bodech a jednostranné limity. . Pravidlo platí i pro limity v nevlastních bodech a jednostranné limity.
| (40) |
|
Příklad 45:
Vypočtěte: 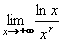
| = |
Jedná se o neurčitý výraz typu 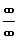
Vypočteme derivaci čitatele a derivaci jmenovatele:
f´(x) = 1/x
g´(x) = r.xr-1
Múžeme tedy l´Hospitalovým pravidlem vypočítat limitu pomocí derivací:
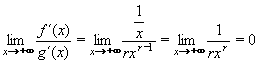 a to je i výsledná, hledaná limita. a to je i výsledná, hledaná limita.
Výsledek: 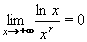
|
I druhé l´Hospitalovo pravidlo lze aplikovat opakovaně, dokonce ho lze kombinovat s prvním pravidlem.
Ostatní typy neurčitých výrazů lze převést na tyto dva typy a počítat je také l´Hospitalovým pravidlem.
Příklad 46:
Vypočtěte: 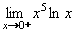
| = |
Jedná se o neurčitý výraz typu 0. , který převedeme na typ , který převedeme na typ
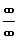 takto: takto:
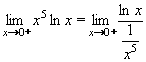
a vypočteme pomocí l´Hospitalova pravidla:
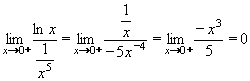
Výsledek: 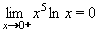
|
Neurčité typy 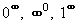 nejprve zlogaritmujeme, potom převedeme na typ nejprve zlogaritmujeme, potom převedeme na typ
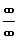 nebo nebo 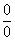 a požijeme
l´Hospitalova pravidla. Nakonec odlogaritmujeme a vypočteme původní limitu. a požijeme
l´Hospitalova pravidla. Nakonec odlogaritmujeme a vypočteme původní limitu.
Příklad 47:
Vypočtěte: 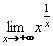
| = |
Jedná se o neurčitý výraz typu 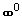 . .
Výraz označíme A a zlogaritmujeme:
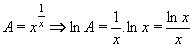 . .
Nyní vypočítáme limitu zlogaritmovaného výrazu l´Hospitalovým pravidlem:
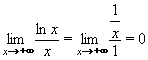
Nakonec odlogaritmujeme a vrátíme se k původní limitě:
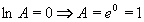
Výsledek: 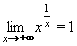
|
Přibližné řešení rovnic
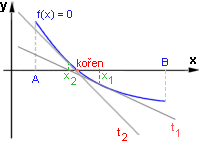 Při numerickém řešení rovnice opakovaně počítáme přibližné hodnoty (aproximace) kořenu a tím se přibližujeme k hodnotě
skutečného kořenu rovnice dokud není dosaženo požadovné přesnosti.
Při numerickém řešení rovnice opakovaně počítáme přibližné hodnoty (aproximace) kořenu a tím se přibližujeme k hodnotě
skutečného kořenu rovnice dokud není dosaženo požadovné přesnosti.
Jednou z používaných metod je Newtonova metoda (metoda tečen).
Jako první aproximaci (x1) kořene rovnice v intervalu <A,B> použijeme střed tohoto intervalu.
V něm sestrojíme tečnu a její průsečík s osou x je novou aproximací (x2) kořene. V tomto bodě sestrojíme
opět tečnu atd.
Další, přesnější, novou aproximaci kořene tedy hledáme jako průsečík tečny ve staré aproximaci
s osou x.
Máme-li řešit rovnici f(x) = 0 , pak rovnice tečny ve starém průsečíku (xn) bude
y - f(xn) = f´(xn)(x - xn)
Průsečík s osou x získáme vyjádřením x z rovnice:
0 - f(xn) = f´(xn)(x - xn) Tedy:
x = xn - f(xn)/f´(xn)
Tento průsečík bude novou aproximací (xn+1) kořene.
Výsledný vztah pro výpočet nové aproximace tedy zní: xn+1 = xn - f(xn)/f´(xn)
Tento proces opakujeme tak dlouho, dokud nedosáhneme požadované přesnosti, tedy dokud
absolutní hodnota rozdílu xn+1 - xn nebude menší než dané číslo - požadovaná přesnost.
Přibližné řešení rovnice f(x) = 0:
Další aproximaci kořene z předchozí vypočteme užitím vztahu: 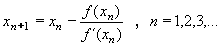
a první aproximaci volíme střed intervalu obsahujícího kořen.
| (41) |
|
Příklad 48:
Najděte přibližně kořen rovnice x4 + x - 1 = 0 v intervalu (0,1)
| = |
Určímen nejprve derivaci funkce f(x) = x4 + x - 1
f'(x) = 4.x3 + 1
První aproximací kořene zvolíme střed intervalu: x1 = 0,5
Druhou aproximaci vypočteme užitím vztahu: x2 = x1 - f(x1)/f´(x1) ,
kde f(x1) = 0,54 + 0,5 - 1 = -0,4375 a f´(x1) = 4.0,53 + 1 = 1,5
tedy x2 = 0,5 + 0,4375/1,5 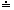 0,7919 0,7919
Třetí aproximaci vypočteme obdobně: x3 = x2 - f(x2)/f´(x2) ,
kde f(x2) = 0,79194 + 0,7919 - 1 = 0,184564 a f´(x2) = 4.0,79193 + 1 = 2,984916
tedy x3 = 0,7919 - 0,184564/2,984916 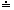 0,72987 0,72987
Čtvrtá aproximace: x4 = x3 - f(x3)/f´(x3) ,
x4 = 0,72987 - 0,0136447/2,555224 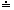 0,72453 0,72453
Tak bychom mohli pokračovat dál a aproximaci kořene upřesňovat.
Abychom odhadli, jaké chyby jsme se dopustili, vypočteme:
f(0,72) 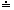 -0,11 < 0 -0,11 < 0
f(0,724) 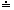 -0,0012 < 0 -0,0012 < 0
f(0,7245) 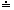 0,00002 > 0 0,00002 > 0
Kořen rovnice je tedy v intervalu (0,724 ; 0,7245) a odhadem chyby naší poslední aproximace x4 je
polovina délky tohoto intervalu, tedy 0,0005/2 = 0,00025
Výsledek: Kořenem rovnice je x = 0,72453 s chybou 0,00025.
|
B. Příklady s krokovou kontrolou e-učitele
C. Příklady na procvičení učiva
Na následujících příkladech s výsledky se můžete zdokonalit ve znalostech učiva této lekce.
Pokud si nevíte s příkladem rady, užijte stručné nápovědy - Help.
| Příklady označené | A mají největší obtížnost, | B střední a | C nejmenší. |
D. Kontrolní test
E.Náhodný test
F. Hodnocení výsledků a komunikace s učitelem (tutorem)
Vytisknout certifikat
Hodnocení výsledků:
Komunikace s učitelem (tutorem):
Tato část je určena pouze pro registrované uživatele. Zaregistrujte se!
|
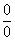 ,
tedy
,
tedy 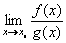 , kde f(xo) = g(xo) = 0. Zkusme se na tento
případ podívat jinak - "derivačně". Vyjádřeme limitu podílu derivací funkcí ve zmíněném bodě xo:
, kde f(xo) = g(xo) = 0. Zkusme se na tento
případ podívat jinak - "derivačně". Vyjádřeme limitu podílu derivací funkcí ve zmíněném bodě xo: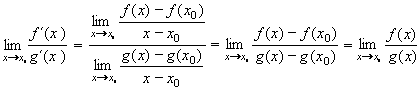 , protože g(xo) = f(xo) = 0
, protože g(xo) = f(xo) = 0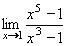
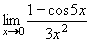
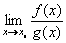 typu
typu 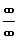 aplikovat druhé l'Hospitalovo pravidlo.
:
aplikovat druhé l'Hospitalovo pravidlo.
: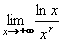
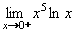
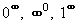 nejprve zlogaritmujeme, potom převedeme na typ
nejprve zlogaritmujeme, potom převedeme na typ
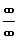 nebo
nebo 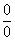 a požijeme
l´Hospitalova pravidla. Nakonec odlogaritmujeme a vypočteme původní limitu.
a požijeme
l´Hospitalova pravidla. Nakonec odlogaritmujeme a vypočteme původní limitu.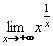
 Při numerickém řešení rovnice opakovaně počítáme přibližné hodnoty (aproximace) kořenu a tím se přibližujeme k hodnotě
skutečného kořenu rovnice dokud není dosaženo požadovné přesnosti.
Při numerickém řešení rovnice opakovaně počítáme přibližné hodnoty (aproximace) kořenu a tím se přibližujeme k hodnotě
skutečného kořenu rovnice dokud není dosaženo požadovné přesnosti.  Označme šířku obdélníkového výběhu x a délku y metrů (podle obrázku).
Vzhledem k délce pletiva platí: 2x + y = 50
Označme šířku obdélníkového výběhu x a délku y metrů (podle obrázku).
Vzhledem k délce pletiva platí: 2x + y = 50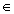 (0,25)
(0,25) Označme poloměr podstavy válcové konzervy r a její výšku v podle obrázku.
Označme poloměr podstavy válcové konzervy r a její výšku v podle obrázku.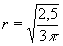 (druhý, opačný nemá pro nás význam).
Vlevo od něho (je to přibližně 0,515) je derivace kladná (V´(0) = 2,5 > 0) a vpravo je záporné (V´(1) = 2,5 - 3.p < 0).
Proto v tomto bodě nastává lokální maximum. Protože je to v intervalu (0,+
(druhý, opačný nemá pro nás význam).
Vlevo od něho (je to přibližně 0,515) je derivace kladná (V´(0) = 2,5 > 0) a vpravo je záporné (V´(1) = 2,5 - 3.p < 0).
Proto v tomto bodě nastává lokální maximum. Protože je to v intervalu (0,+ ) jediný
extrém, je zároveň i globální maximum této funkce. Poloměr požadované konzervy je tedy přesně
) jediný
extrém, je zároveň i globální maximum této funkce. Poloměr požadované konzervy je tedy přesně 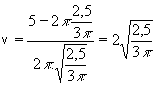 (což je přibližně 1,03 dm).
(což je přibližně 1,03 dm).  0 a existuje limita
0 a existuje limita
 , pak je to i hledaná limita, tedy platí:
, pak je to i hledaná limita, tedy platí:
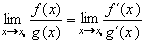
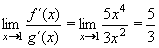 a to je i výsledná, hledaná limita.
a to je i výsledná, hledaná limita.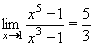
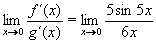 dostáváme opět neurčitý výraz typu
dostáváme opět neurčitý výraz typu 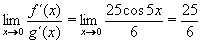 a tím dostáváme i výslednou, hledanou limitu.
a tím dostáváme i výslednou, hledanou limitu.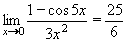
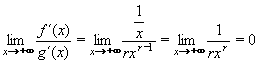 a to je i výsledná, hledaná limita.
a to je i výsledná, hledaná limita.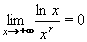
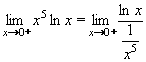
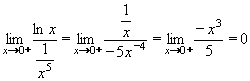
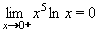
 .
.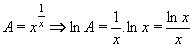 .
.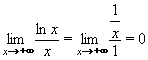
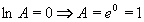
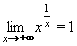
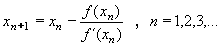
 0,7919
0,7919