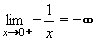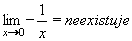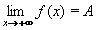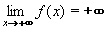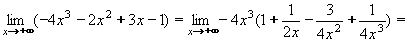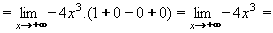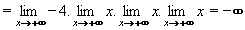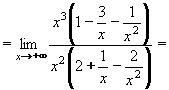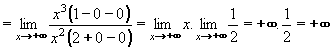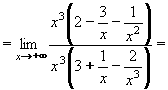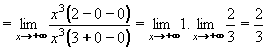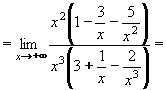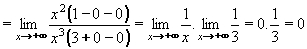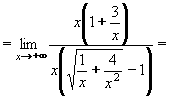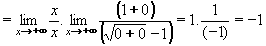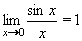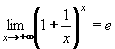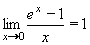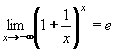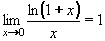| Matika krokem - 2.lekce ... |
|
Limita, derivace a integrál 2.lekce - Jednostranná a nevlastní limita |
Vytisknout |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Skype výuka, doučování |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
A. Výklad a ukázkové příklady
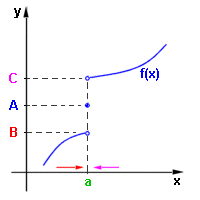 Jednostranné limity
Jednostranné limityZatím jsme nerozlišovali, zda se hodnoty proměnné x k bodu a přibližují zprava (od větších hodnot) nebo zleva (od menších hodnot), protože to nehrálo žádnou roli, bylo to v obou případech stejné. Existují však příklady funkcí, kdy je třeba rozlišovat, zda se k danému bodu a přibližujeme zprava nebo zleva. Začneme opět příkladem. Na obrázku máme funkci f: y = f(x), která má v bodě a hodnotu f(a) = A, ale číslo A není limitou f(x) v bodě a (není v bodě a spojitá). Blížíme-li se k bodu a zleva ( x < a ) , blíží se hodnota funkce f(x) (zřejmé z grafu) číslu B. Říkame, že funkce y = f(x) má v bodě a limitu zleva číslo B a zapisujeme: 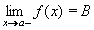 Blížíme-li se k bodu a zprava ( x > a ) , blíží se hodnota funkce f(x) číslu C. Říkame, že funkce y = f(x) má v bodě a limitu zprava číslo C a zapisujeme: 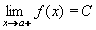 Těmto limitám také říkáme jednostranné limity v bodě a. Při matematickém vyjádření se proti obecné definici limity (lekce 1) změní pouze posuzování "blízkosti" k bodu a. Budeme-li se přibližovat zleva, hodnoty x budou patřit do intervalu (a - d,a), tedy platí 0 < a - x < d (viz obrázek - levá část původního intervalu). Při přibližování zprava budou hodnoty x patřit do intervalu (a,a + d) a tedy platí 0 < x - a < d. 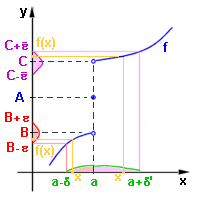
Souvislost mezi limitou funkce v bodě a a jednostrannými limitami v bodě a upřesňuje následující (zřejmá) věta:
Naše funkce f na obrázku má limitu v bodě a zleva i zprava, ale protože si nejsou rovny, nemá limitu v bodě a. Pokud je nějaká funkce f v bodě a spojitá, pak se obě jednostrané limity rovnají funkční hodnotě v bodě a. Příklad 10:Vypočtěte: 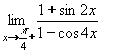
Příklad 11:Vypočtěte: 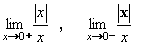
Nevlastní limity 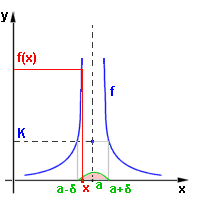 Limitou funkce v daném bodě a nemusí být vždy konečné reálné číslo.
Limitou funkce v daném bodě a nemusí být vždy konečné reálné číslo. Mějme například funkci f: y = x-2. Pokud se přibližujeme k bodu x = 0 ať už zleva nebo zprava, hodnoty funkce rostou nade všechny meze. Říkáme také, že má funkce f v bodě x = 0 nevlastní limitu (na rozdíl od těch konečných, kterým říkáme vlastní). Co to matematicky znamená, že hodnoty funkce rostou nade všechny meze? Nabývá funkce při přibližování k 0 hodnot větších než 10000? Ano, pro x z intervalu (-10-2,0)U(0,10-2) bude y = x-2 > 10000 . Ke každému kladnému číslu K lze nalézt hodnoty x z "blízkosti" bodu x = 0 pro které bude funkce nabývat hodnot ještě větších než číslo K.
Podobně můžeme definovat nevlastní limitu +  v bodě a zleva (změní se v definici
pouze formulace ...pro všechna x, pro která platí 0 < a - x < d ... nebo zprava (změní se v definici
formulace ...pro všechna x, pro která platí 0 < x - a < d ... . v bodě a zleva (změní se v definici
pouze formulace ...pro všechna x, pro která platí 0 < a - x < d ... nebo zprava (změní se v definici
formulace ...pro všechna x, pro která platí 0 < x - a < d ... .Analogicky zavádíme nevlastní limitu -  . .V definici (14) se změmí pouze ...ke každému zápornému číslu K .... ... je f(x) < K. Podobně můžeme definovat nevlastní limitu -  v bodě a zleva (změní se v definici
pouze formulace ...pro všechna x, pro která platí 0 < a - x < d ... nebo zprava (změní se v definici
formulace ...pro všechna x, pro která platí 0 < x - a < d ... . v bodě a zleva (změní se v definici
pouze formulace ...pro všechna x, pro která platí 0 < a - x < d ... nebo zprava (změní se v definici
formulace ...pro všechna x, pro která platí 0 < x - a < d ... .Ukažme si konkrétní příklady na výpočet jednostranných a nevlastních limit.
Příklad 12:Určete limity funkcí f: y = 1/x v bodě x = 0 zleva, zprava.
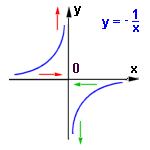
Příklad 13:Určete limity funkcí g: y = -1/x v bodě x = 0 zleva, zprava.
Tyto limity je užitečné si zapamatovat!. Limita v nevlastním bodě 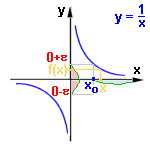 Nyní nás nebude zajímat limita v určitém, konkrétním bodě a, ale pro x blížící se k +
Nyní nás nebude zajímat limita v určitém, konkrétním bodě a, ale pro x blížící se k + nebo - nebo - ,
tedy v nevlastním bodě. Tato limita může být vlastní (konečná) nebo nevlastní (nekonečná). ,
tedy v nevlastním bodě. Tato limita může být vlastní (konečná) nebo nevlastní (nekonečná).Tak například pro funkci f: y = 1/x platí: jestliže se bude x neustále zvětšovat (100 ; 1000 ; 10000) , budou se kladné hodnoty y = 1/x neustále zmenšovat (1/100 ; 1/1000 ; 1/10000), tedy pro x neomezeně rostoucí se budou hodnoty funkce neomezeně blížit k číslu 0. Je tedy limita funkce f v nevlastním bodě +  rovna 0.
Zápis: rovna 0.
Zápis: 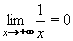 Intuitivně tedy k libovolně zvolené "blízkosti" k číslu 0 (1/100 ; 1/1000 ; 1/10000) lze nalézt odpovídající hodnotu x0 (100 ; 1000 ; 10000), tak že pro ještě větší x (větší než x0) budou hodnoty y = 1/x ještě bližší k číslu 0. Matematicky a obecně:
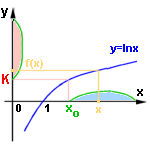 Obdobně lze definovat v nevlastním bodě nevlastní limitu (tedy limitu +
Obdobně lze definovat v nevlastním bodě nevlastní limitu (tedy limitu + nebo -+ nebo -+ ). ).Tak například pro funkci f: y = lnx platí: jestliže se bude x neustále zvětšovat (nade všechny meze) , budou se kladné hodnoty y = lnx také zvětšovat (nade všehny meze), tedy pro x neomezeně rostoucí budou hodnoty funkce také neomezeně růst0. Je tedy limita funkce f v nevlastním bodě +  rovna + rovna + .
Zápis: .
Zápis: 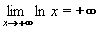 Intuitivně tedy k libovolně velkému číslu K lze vždy nalézt odpovídající bod (hodnotu) x0 tak, že pro hodnoty x větší než x0 budou hodnoty funkce ještě větší než číslo K. Matematicky a obecně:
Ukážeme si několik příkladů výpočtu limity v nevlastním bodě. Příklad 14:Vypočtěte: 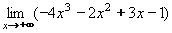
Příklad 15:Vypočtěte: 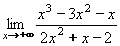
Příklad 16:Vypočtěte: 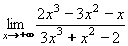
Příklad 17:Vypočtěte: 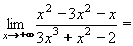
Je-li tedy stupeň polynomu v čitateli větší než ve jmenovateli, výsledkem je nevlastní limita, jso-li stupně stejné, je výsledná limita vlastní (konečná) a je-li stupeň jmenovatele větší, výsledná limita je číslo 0. Příklad 18:Vypočtěte: 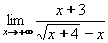
Výpočet limit nám umožní a usnadní zapamtování některých důležitých, základních limit. Patří mezi ně například:
B. Příklady s krokovou kontrolou e-učitele C. Příklady na procvičení učiva Na následujících příkladech s výsledky se můžete zdokonalit ve znalostech učiva této lekce. Pokud si nevíte s příkladem rady, užijte stručné nápovědy - Help.
D. Kontrolní test E.Náhodný test F. Hodnocení výsledků a komunikace s učitelem (tutorem) Komunikace s učitelem (tutorem): Tato část je určena pouze pro registrované uživatele. Zaregistrujte se! |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
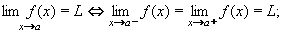
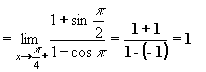
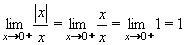
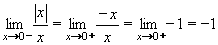
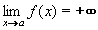
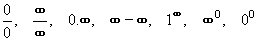 - nazýváme je neurčité výraz -
potom musíme neurčitý výraz odstranit, např. po úpravách funkci nahradit funkcí spojitou (podle věty o limitě dvou funkcí).
Pokud nedostaneme neurčitý výraz, často pomůže graf příslušné funkce nebo dosazování několika "přibližujících se" bodů.
- nazýváme je neurčité výraz -
potom musíme neurčitý výraz odstranit, např. po úpravách funkci nahradit funkcí spojitou (podle věty o limitě dvou funkcí).
Pokud nedostaneme neurčitý výraz, často pomůže graf příslušné funkce nebo dosazování několika "přibližujících se" bodů.
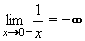
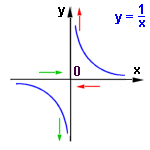 Jestliže se bude x zprava přibližovat k 0 (hodnoty x budou kladné a stále v abs.hodnotě menší ... např. 0,1 ; 0,01 ; 0,001 ... )
budou se hodnoty y = 1/x neustále zvětšovat (10 ; 100 ; 1000). Je tedy limita této funkce v bodě x = 0 zprava rovna +
Jestliže se bude x zprava přibližovat k 0 (hodnoty x budou kladné a stále v abs.hodnotě menší ... např. 0,1 ; 0,01 ; 0,001 ... )
budou se hodnoty y = 1/x neustále zvětšovat (10 ; 100 ; 1000). Je tedy limita této funkce v bodě x = 0 zprava rovna +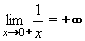
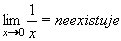
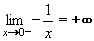
 Jestliže se bude x zprava přibližovat k 0 (hodnoty x budou kladné a stále v abs.hodnotě menší ... např. 0,1 ; 0,01 ; 0,001 ... )
budou se hodnoty y = -1/x neustále zmenšovat (-10 ; -100 ; -1000). Je tedy limita této funkce v bodě x = 0 zprava rovna -
Jestliže se bude x zprava přibližovat k 0 (hodnoty x budou kladné a stále v abs.hodnotě menší ... např. 0,1 ; 0,01 ; 0,001 ... )
budou se hodnoty y = -1/x neustále zmenšovat (-10 ; -100 ; -1000). Je tedy limita této funkce v bodě x = 0 zprava rovna -