Matika krokem - 5.lekce

Matika krokem - 5.lekce ...

Komplexní čísla
5.lekce - Řešení rovnic v oboru komplexních čísel

A. Výklad a ukázkové příklady

Kvadratická rovnice s reálnými koeficienty

Kvadratická rovnice s reálnými koeficienty a,b,c nemá v oboru reálných čísel pro záporný diskriminant (D<0) reálné řešení (neexistuje reálná odmocnina ze záporného čísla). V oboru komplexních čísel lze ale dokázat, že platí:

Odmocnina z čísla -D (kladné) již existuje a dostáváme závěr:

Kvadratická rovnice ax² + bx + c = 0 s reálnými koeficienty a záporným diskriminantem D má v oboru komplexních čísel právě dva kořeny, a to sdružená imaginární čísla:

(17)

Příklad 1: V oboru komplexních čísel řešte rovnici 3x² - 4x + 2 = 0.

=	D = 16 - 24 = -8

Příklad 2: V oboru komplex.čísel řešte rovnici (p - 1)x² - (p - 2)x + 2p - 1 = 0 s neznámou x a s real.parametrem p.

Množinu kořenů K rovnice v závislosti na parametru p shrnuje tabulka:

p	K
(-,0)
0	x_1,2 = 1
(0,1)
1	x = -1
(1,8/7)
8/7	x_1,2 = -3
(8/7,+)

Protože je každá kvadratická rovnice s reálnými koeficienty v oboru komplexních čísel řešitelná (existují její kořeny), lze i každý kvadratický trojčlen s reálnými koeficienty rozložit v součin a platí:

Každý kvadratický trojčlen ax² + bx + c s reálnými koeficienty lze vyjádřit jako součin:
ax² + bx + c = a(x - x₁)(x - x₂) ,
kde x₁, x₂ jsou kořeny rovnice ax² + bx + c = 0.

(18)

Příklad 3: Rozložte v součin lineárních činitelů kvadratický trojčlen x² - 6x + 13.

=	Nejprve určíme kořeny odpovídající rovnice x² - 6x + 13 = 0. D = 36 - 52 = -16 A nyní můžeme rozložit: x² - 6x + 13 = (x - 3 + 2i)(x - 3 -2i)

Binomické rovnice

Binomická rovnice je rovnice tvaru xⁿ - a = 0
kde a je komplexní číslo , x neznámá a n je přirozené číslo větší než 1.

(19)

Obě čísla převedeme do goniometrického tvaru, použijeme Moivreovy věty a dostáváme:
|x|ⁿ(cosnf+isinnf) = |a|(cosa+isina)
Číslo x je tedy komplexní n-tou odmocninou čísla a (kořenem binomické rovnice) a platí:

Binomická rovnice xⁿ - |a|(cosa+isina) = 0
má v oboru komplexních čísel právě n různých kořenů:

, k = 0, 1, 2, ..., n-1

(20)

Tyto kořeny leží (pro n>2) v Gaussově rovině ve vrcholech pravidelného n-úhelníka vepsaného do kružnice se středem v počátku a s poloměrem

. Argumenty kořenů se liší o

(každý další dostaneme přičtením

)

Při odmocňování tedy absolutní hodnotu odmocníme a argument dělíme odmocnitelem. Odmocnin je n a každou další dostaneme přičtením

k argumentu.

Příklad 4: V množině komplexních čísel řešte rovnici x⁴ + 1 + i = 0 .

Upravíme:
x⁴ = -1 - i
číslo -1 - i převedeme do goniometrického tvaru:

Nyní určíme čtvrtou odmocninu z tohoto čísla. Obecně vypadá pro k = 0,1,2,3:

a po rozepsání pro jednotlivá k (přičítáme k argumentům

) , máme čtyři kořeny (odmocniny):

.
Obrazy těchto čísel v Gaussově rovině leží ve vrcholech (n=4) čtverce podle obrázku:

Kořeny zvláštního případu binomické rovnice xⁿ - 1 = 0 jsou komplexní jednotky a jejich obrazy leží ve vrcholech pravidelného n-úhelníku vepsaného do jednotkové kružnice se středem v počátku. Jeden z vrcholů leží v bodě 1 na reálné ose.

Kvadratická rovnice s komplexními koeficienty

Kvadratickou rovnici s komplexními koeficienty ax² + bx + c = 0 , řešíme podle známého vzorce

, kde a,b,c,D jsou ale komplexní čísla. Proto bývá největším problémem výpočet druhé odmocniny diskriminantu. Nejčastěji se diskriminant převede do goniometrického tvaru a potom odmocní jak bylo uvedeno při výpočtu odmocniny (u binomické rovnice).

(21)

Komplexní čísla, která jsou kořeny rovnice, nemusí být sdružená. Sdružená jsou v případě reálných koeficientů a záporného diskriminantu.

Příklad 5: V množině komplexních čísel řešte rovnici (1-i)x² - (5-i)x + 6 - 4i = 0 .

=	Diskriminant rovnice je D = (5-i)² - 4(1-i)(6-4i) = 16 + 30i = 34(cos61,927513..^o +isin61,927513..^o) . (cos30,963757..^o + isin30,963757..^o) = 5 + 3i. Kořeny tedy jsou a po odstranění závorek a vydělení komplexních čísel dostaneme výsledné kořeny: x₁ = 2 + 3i a x₂ = 1 - i

Druhou odmocninu z komplexního čísla můžeme také počítat bez převodu do goniometrického tavru. Jako výsledek odmocniny položíme x + iy (je to zase komplexní číslo), umocníme obě strany rovnice na druhou, porovnáním částí kompl.čísel získáme soustavu rovnic, ze které získáme hledané kompl.číslo.

(22)

Příklad 6: Vypočítejte druhou odmocninu komplexního čísla 16 + 30i

Výsledkem musí být komplexní číslo, položime tedy:

Umocníme obě strany rovnice na druhou:
x² + 2ixy - y² = 16 + 30i
Porovnáním reálných částí a imaginárních částí dostáváme soustavu rovnic:
x² - y² = 16 a současně 2xy = 30
Substituční metodou po vyjádření y = 15/x dostáváme rovnici:
x⁴ - 16 x² - 225 = 0
Ta dává reálné řešení x=5 nebo x=-5 a po dosazení y = 3 nebo y = -3.
Výsledkem jsou tedy dvě čísla: 5 + 3i , -5 - 3i

Stejně jako pro kvadratický trojčlen s reálnými koeficienty platí i zde:

Každý kvadratický trojčlen ax² + bx + c s komplexními koeficienty lze vyjádřit jako součin:
ax² + bx + c = a(x - x₁)(x - x₂) ,
kde x₁, x₂ jsou kořeny rovnice ax² + bx + c = 0.

(23)

Příklad 7: Rozložte kvadratický trojčlen (1-i)x² - (5-i)x + 6 - 4i .

=	V předchozím příkladě jsme určili kořeny odpovídající rovnice a proto můžeme tedy ihned psát: (1-i)x² - (5-i)x + 6 - 4i = (1-i)(x-2-3i)(x-1+i)

A to již konec kurzu Komplexní čísla.

Přehled použité a doporučené literatury:
PhDr.Ivan Bušek - Řešené maturitní úlohy z matematiky, SPN 1988
Petr Benda a kol. - Sbírka maturitních příkladů z matematiky, SPN 1983
Doc.RNDr.Emil Calda, Csc. - Matematika pro gymnázia - Komplexní čísla, Prometheus 1997
František Vejsada, František Talafous - Sbírka úloh z matematiky pro gymnázia, SPN 1969

B. Příklady s krokovou kontrolou e-učitele

C. Příklady na procvičení učiva

Na následujících příkladech s výsledky se můžete zdokonalit ve znalostech učiva této lekce.
Pokud si nevíte s příkladem rady, užijte stručné nápovědy - Help.

Příklady označené

A mají největší obtížnost,

B střední a

C nejmenší.

1	V množině C řešte rovnici a kořeny znázorněte geometricky: z³ - 8 = 0	C	Help	Výsledek
2	Vypočtěte a znázorněte druhé odmocniny kompl.čísel: z = -6 - 8i	B	Help	Výsledek
3	V množině C řešte rovnici a kořeny znázorněte geometricky: z³ + 8 = 0	C	Help	Výsledek
4	Vypočtěte a znázorněte druhé odmocniny kompl.čísel: z = 4i - 3	B	Help	Výsledek
5	V množině C řešte rovnici: (z⁴+1)² + 2(z⁴+1) - 8 = 0	A	Help	Výsledek
6	V množině C řešte rovnici: z⁶ - 7z³ - 8 = 0	B	Help	Výsledek
7	Zapište aspoň jednu kvadratickou rovnici, jejíž kořeny v C jsou: x₁ = 1/2 - i , x₂ = 1/2 + i	C	Help	Výsledek
8	V množině C řešte rovnici: z⁸ + z⁴ - 20 = 0	B	Help	Výsledek
9	V množině C řešte rovnici:	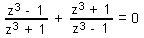A	Help	Výsledek
10	V množině C řešte rovnici: (z³ + i)(z³ + 8) = 0	B	Help	Výsledek
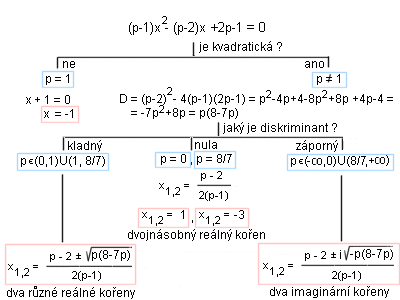
11	V množině C řešte rovnici s reálným parametrem p: px² + 2(p - 1)x + p - 5 = 0	A	Help	Výsledek
12	V množině C řešte rovnici: (z⁴ - 4)(z⁶ + i) = 0	B	Help	Výsledek
13	V množině C řešte rovnici: z² - 2(3 - i)z + 7 - 6i = 0	A	Help	Výsledek
14	V množině C řešte rovnici: z² - 2(1 + i)z + 2i = 0	B	Help	Výsledek
15	V množině C řešte rovnici s reálným parametrem p: x² + 2px + 25 = 0	A	Help	Výsledek
16	V množině C řešte rovnici: (z² + 1)(z² - 1)(z² + i)(z² - i) = 0	B	Help	Výsledek
17	V množině C řešte rovnici s reálným parametrem p: (p + 3)x² + 3(p - 6)x + 5 - 18p = 0	A	Help	Výsledek
18	V množině C řešte rovnici: (z⁶ + 64)(z⁶ - 16) = 0	B	Help	Výsledek
19	V množině C řešte rovnici: 4x² + 3 = 0	C	Help	Výsledek
20	V množině C řešte rovnici: z² - 6iz - 8 = 0	B	Help	Výsledek
21	Zapište aspoň jednu kvadratickou rovnici, jejíž kořeny v C jsou: x₁ = -1 - 2i , x₂ = 1 - 2i	C	Help	Výsledek
22	V množině C řešte rovnici:	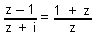B	Help	Výsledek
23	V množině C řešte rovnici a kořeny znázorněte geometricky: z⁸ + 1 = 0	C	Help	Výsledek
24	V množině C řešte rovnici: z² - 4i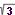z - 9 = 0	B	Help	Výsledek
25	V množině C řešte rovnici: x² - 3x + 3 = 0	C	Help	Výsledek
26	V množině C řešte rovnici:	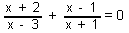B	Help	Výsledek
27	V množině C řešte rovnici: 2x² + x + 1 = 0	C	Help	Výsledek
28	Rozložte v součiny lineárních dvojčlenů trojčleny: 3x² + 2x + 2	B	Help	Výsledek
29	V množině C řešte jako rovnici kvadratickou i jako binomickou: z² - 2z + 4 = 0	C	Help	Výsledek
30	V množině C řešte rovnici s reálným parametrem p: px² + (2p - 1)x + p = 0	A	Help	Výsledek
31	V množině C řešte jako rovnici kvadratickou i jako binomickou: z² + 2z + 2 = 0	C	Help	Výsledek
32	Rozložte v součiny lineárních dvojčlenů trojčleny: x² + x + 1	B	Help	Výsledek
33	V množině C řešte rovnici: 3x² - 7x + 5 = 0	C	Help	Výsledek
34	Rozložte v součiny lineárních dvojčlenů trojčleny: x² - x + 1	B	Help	Výsledek
35	V množině C řešte rovnici: (x² + x + 1)(x² + x - 1) = 0	C	Help	Výsledek
36	Rozložte v součiny lineárních dvojčlenů trojčleny: x² - 3x + 5	B	Help	Výsledek
37	V množině C řešte rovnici a kořeny znázorněte geometricky: z³ - i = 0	C	Help	Výsledek
38	V množině C řešte rovnici a kořeny znázorněte geometricky: z⁵ - 1 - i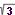 = 0	B	Help	Výsledek
39	V množině C řešte rovnici a kořeny znázorněte geometricky: z³ + i = 0	C	Help	Výsledek
40	V množině C řešte rovnici a kořeny znázorněte geometricky: z⁵ + 1 - i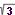 = 0	B	Help	Výsledek
41	V množině C řešte rovnici a kořeny znázorněte geometricky: z⁶ + 64 = 0	C	Help	Výsledek
42	V množině C řešte rovnici: z² - 4 = 3i	A	Help	Výsledek
43	V množině C řešte rovnici a kořeny znázorněte geometricky: z³ - 1 + i = 0	B	Help	Výsledek
44	V množině C řešte rovnici a kořeny znázorněte geometricky: z⁶ - 64 = 0	C	Help	Výsledek
45	V množině C řešte rovnici: z² + (2-3i)z - 5(1+i) = 0	A	Help	Výsledek
46	V množině C řešte rovnici a kořeny znázorněte geometricky: z³ + 1 - i = 0	B	Help	Výsledek
47	V množině C řešte rovnici a kořeny znázorněte geometricky: z⁴ - 1 = 0	C	Help	Výsledek
48	V množině C řešte jako rovnici kvadratickou i jako binomickou: z² - 2z + 2 = 0	A	Help	Výsledek
49	V množině C řešte rovnici a kořeny znázorněte geometricky: z⁴ + 1 = 0	C	Help	Výsledek
50	V množině C řešte rovnici: z² - 2z + 9 + 6i = 0	A	Help	Výsledek
51	V množině C řešte jako rovnici kvadratickou i jako binomickou: z² + 1 = 0	B	Help	Výsledek
52	V množině C řešte rovnici a kořeny znázorněte geometricky: z⁸ - 1 = 0	C	Help	Výsledek
53	V množině C řešte rovnici: z² + 3z + 10i = 0	A	Help	Výsledek
54	V množině C řešte rovnici:	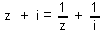B	Help	Výsledek
55	V množině C řešte soustavu rovnic: 2x - y = 1 + 3i , xy = 2	A	Help	Výsledek
56	V množině C řešte rovnici:	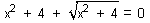B	Help	Výsledek
57	Určete komplexní číslo p tak, aby rovnice: x² - 2(3+i)x + p = 0 měla jediný kořen.	C	Help	Výsledek
58	V množině C řešte soustavu rovnic: x² + y² = 1 , x - y = -2	A	Help	Výsledek
59	V množině C řešte rovnici: x⁶ - 19x³ - 216 = 0	B	Help	Výsledek
60	V množině C řešte rovnici:	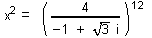A	Help	Výsledek
61	V množině C řešte rovnici: x⁶ + 19x³ - 216 = 0	B	Help	Výsledek
62	V množině C řešte rovnici:	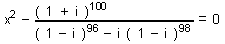A	Help	Výsledek
63	V množině C řešte rovnici: x⁴ - 2 + 2i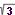 = 0	B	Help	Výsledek
64	V množině C řešte rovnici: ix² + 3(3-2i)x - 6 = 0	A	Help	Výsledek
65	V množině C řešte rovnici: x⁶ + 3 = 0	B	Help	Výsledek
66	V množině C řešte rovnici: ix² + 2(i-1)x + 3 + 2i = 0	A	Help	Výsledek
67	V množině C řešte rovnici: x⁴ + 2 + 2i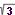 = 0	B	Help	Výsledek
68	V množině C řešte rovnici:	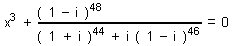A	Help	Výsledek
69	V množině C řešte rovnici s reálným parametem p: x² - 2(p + 4)x + p² + 6p = 0	B	Help	Výsledek
70	V množině C řešte rovnici: (x + 1)⁴ = 81x⁴	A	Help	Výsledek
71	V množině C řešte rovnici s reálným parametem p: px² + 2(p - 1)x + p - 5 = 0	B	Help	Výsledek
72	V množině C řešte rovnici: (x³ - 1)² + (x³ + 1)² = 0	A	Help	Výsledek
73	V množině C řešte rovnici: (x² + 3x + 5)(x² + 3x + 6)(x² + 3x + 7) = 0	B	Help	Výsledek
74	V množině C řešte rovnici: (x⁴ + 1)² + 2(x⁴ + 1) - 8 = 0	A	Help	Výsledek
75	V množině C řešte rovnici: (x² + 4)(x² -i) = 0	B	Help	Výsledek
76	V množině C řešte rovnici:	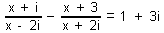A	Help	Výsledek
77	V množině C řešte rovnici:	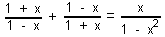B	Help	Výsledek
78	V množině C řešte rovnici: 16x⁴ = (x - 1)⁴	A	Help	Výsledek
79	V množině C řešte rovnici:	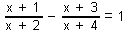B	Help	Výsledek
80	V množině C řešte rovnici: x² + 18 - 6i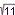 = 0	A	Help	Výsledek
81	Rozložte v C v součiny kvadratické trojčleny: x² - 2x + 1	B	Help	Výsledek
82	V množině C řešte rovnici: x² - 4 - i = 0	A	Help	Výsledek
83	Rozložte v C v součiny kvadratické trojčleny: x² + 4x + 13	B	Help	Výsledek
84	V množině C řešte rovnici: x² + 6 + 8i = 0	A	Help	Výsledek
85	Rozložte v C v součiny kvadratické trojčleny: x² - (-2 + i)x - 2i	A	Help	Výsledek
86	V množině C řešte soustavu rovnic: x + y = -i , x² + y² = 1	B	Help	Výsledek
87	Rozložte v C v součiny kvadratické trojčleny: x² + 5 + 12i	A	Help	Výsledek
88	V množině C řešte rovnici: x⁴ - 4x³+ 6x² - 4x = 80	A	Help	Výsledek
89	V množině C řešte soustavu rovnic: x + y = -i , x² + y² = -1	B	Help	Výsledek
90	V množině C řešte rovnici: x³ + 3x² + 3x = 7	A	Help	Výsledek
91	V množině C řešte rovnici: x⁴ - 2x³ + 3x² - 2x + 2 = 0 , víte-li, že má kořen x=i	A	Help	Výsledek
92	V množině C řešte rovnici a kořeny znázorněte geometricky: z³ - 8 = 0	C	Help	Výsledek
93	Vypočtěte a znázorněte druhé odmocniny kompl.čísel: z = -6 - 8i	B	Help	Výsledek
94	V množině C řešte rovnici a kořeny znázorněte geometricky: z³ + 8 = 0	C	Help	Výsledek
95	Vypočtěte a znázorněte druhé odmocniny kompl.čísel: z = 4i - 3	B	Help	Výsledek
96	V množině C řešte rovnici: (z⁴+1)² + 2(z⁴+1) - 8 = 0	A	Help	Výsledek
97	V množině C řešte rovnici: z⁶ - 7z³ - 8 = 0	B	Help	Výsledek
98	Zapište aspoň jednu kvadratickou rovnici, jejíž kořeny v C jsou: x₁ = 1/2 - i , x₂ = 1/2 + i	C	Help	Výsledek
99	V množině C řešte rovnici: z⁸ + z⁴ - 20 = 0	B	Help	Výsledek
100	V množině C řešte rovnici:	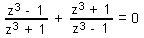A	Help	Výsledek
101	V množině C řešte rovnici: (z³ + i)(z³ + 8) = 0	B	Help	Výsledek
102	V množině C řešte rovnici s reálným parametrem p: px² + 2(p - 1)x + p - 5 = 0	A	Help	Výsledek
103	V množině C řešte rovnici: (z⁴ - 4)(z⁶ + i) = 0	B	Help	Výsledek
104	V množině C řešte rovnici: z² - 2(3 - i)z + 7 - 6i = 0	A	Help	Výsledek
105	V množině C řešte rovnici: z² - 2(1 + i)z + 2i = 0	B	Help	Výsledek
106	V množině C řešte rovnici s reálným parametrem p: x² + 2px + 25 = 0	A	Help	Výsledek
107	V množině C řešte rovnici: (z² + 1)(z² - 1)(z² + i)(z² - i) = 0	B	Help	Výsledek
108	V množině C řešte rovnici s reálným parametrem p: (p + 3)x² + 3(p - 6)x + 5 - 18p = 0	A	Help	Výsledek
109	V množině C řešte rovnici: (z⁶ + 64)(z⁶ - 16) = 0	B	Help	Výsledek
110	V množině C řešte rovnici: 4x² + 3 = 0	C	Help	Výsledek
111	V množině C řešte rovnici: z² - 6iz - 8 = 0	B	Help	Výsledek
112	Zapište aspoň jednu kvadratickou rovnici, jejíž kořeny v C jsou: x₁ = -1 - 2i , x₂ = 1 - 2i	C	Help	Výsledek
113	V množině C řešte rovnici:	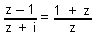B	Help	Výsledek
114	V množině C řešte rovnici a kořeny znázorněte geometricky: z⁸ + 1 = 0	C	Help	Výsledek
115	V množině C řešte rovnici: z² - 4i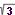z - 9 = 0	B	Help	Výsledek
116	V množině C řešte rovnici: x² - 3x + 3 = 0	C	Help	Výsledek
117	V množině C řešte rovnici:	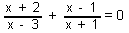B	Help	Výsledek
118	V množině C řešte rovnici: 2x² + x + 1 = 0	C	Help	Výsledek
119	Rozložte v součiny lineárních dvojčlenů trojčleny: 3x² + 2x + 2	B	Help	Výsledek
120	V množině C řešte jako rovnici kvadratickou i jako binomickou: z² - 2z + 4 = 0	C	Help	Výsledek
121	V množině C řešte rovnici s reálným parametrem p: px² + (2p - 1)x + p = 0	A	Help	Výsledek
122	V množině C řešte jako rovnici kvadratickou i jako binomickou: z² + 2z + 2 = 0	C	Help	Výsledek
123	Rozložte v součiny lineárních dvojčlenů trojčleny: x² + x + 1	B	Help	Výsledek
124	V množině C řešte rovnici: 3x² - 7x + 5 = 0	C	Help	Výsledek
125	Rozložte v součiny lineárních dvojčlenů trojčleny: x² - x + 1	B	Help	Výsledek
126	V množině C řešte rovnici: (x² + x + 1)(x² + x - 1) = 0	C	Help	Výsledek
127	Rozložte v součiny lineárních dvojčlenů trojčleny: x² - 3x + 5	B	Help	Výsledek
128	V množině C řešte rovnici a kořeny znázorněte geometricky: z³ - i = 0	C	Help	Výsledek
129	V množině C řešte rovnici a kořeny znázorněte geometricky: z⁵ - 1 - i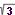 = 0	B	Help	Výsledek
130	V množině C řešte rovnici a kořeny znázorněte geometricky: z³ + i = 0	C	Help	Výsledek
131	V množině C řešte rovnici a kořeny znázorněte geometricky: z⁵ + 1 - i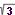 = 0	B	Help	Výsledek
132	V množině C řešte rovnici a kořeny znázorněte geometricky: z⁶ + 64 = 0	C	Help	Výsledek
133	V množině C řešte rovnici: z² - 4 = 3i	A	Help	Výsledek
134	V množině C řešte rovnici a kořeny znázorněte geometricky: z³ - 1 + i = 0	B	Help	Výsledek
135	V množině C řešte rovnici a kořeny znázorněte geometricky: z⁶ - 64 = 0	C	Help	Výsledek
136	V množině C řešte rovnici: z² + (2-3i)z - 5(1+i) = 0	A	Help	Výsledek
137	V množině C řešte rovnici a kořeny znázorněte geometricky: z³ + 1 - i = 0	B	Help	Výsledek
138	V množině C řešte rovnici a kořeny znázorněte geometricky: z⁴ - 1 = 0	C	Help	Výsledek
139	V množině C řešte jako rovnici kvadratickou i jako binomickou: z² - 2z + 2 = 0	A	Help	Výsledek
140	V množině C řešte rovnici a kořeny znázorněte geometricky: z⁴ + 1 = 0	C	Help	Výsledek
141	V množině C řešte rovnici: z² - 2z + 9 + 6i = 0	A	Help	Výsledek
142	V množině C řešte jako rovnici kvadratickou i jako binomickou: z² + 1 = 0	B	Help	Výsledek
143	V množině C řešte rovnici a kořeny znázorněte geometricky: z⁸ - 1 = 0	C	Help	Výsledek
144	V množině C řešte rovnici: z² + 3z + 10i = 0	A	Help	Výsledek
145	V množině C řešte rovnici:	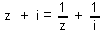B	Help	Výsledek
146	V množině C řešte soustavu rovnic: 2x - y = 1 + 3i , xy = 2	A	Help	Výsledek
147	V množině C řešte rovnici:	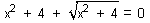B	Help	Výsledek
148	Určete komplexní číslo p tak, aby rovnice: x² - 2(3+i)x + p = 0 měla jediný kořen.	C	Help	Výsledek
149	V množině C řešte soustavu rovnic: x² + y² = 1 , x - y = -2	A	Help	Výsledek
150	V množině C řešte rovnici: x⁶ - 19x³ - 216 = 0	B	Help	Výsledek
151	V množině C řešte rovnici:	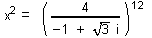A	Help	Výsledek
152	V množině C řešte rovnici: x⁶ + 19x³ - 216 = 0	B	Help	Výsledek
153	V množině C řešte rovnici:	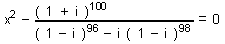A	Help	Výsledek
154	V množině C řešte rovnici: x⁴ - 2 + 2i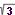 = 0	B	Help	Výsledek
155	V množině C řešte rovnici: ix² + 3(3-2i)x - 6 = 0	A	Help	Výsledek
156	V množině C řešte rovnici: x⁶ + 3 = 0	B	Help	Výsledek
157	V množině C řešte rovnici: ix² + 2(i-1)x + 3 + 2i = 0	A	Help	Výsledek
158	V množině C řešte rovnici: x⁴ + 2 + 2i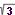 = 0	B	Help	Výsledek
159	V množině C řešte rovnici:	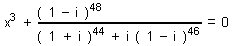A	Help	Výsledek
160	V množině C řešte rovnici s reálným parametem p: x² - 2(p + 4)x + p² + 6p = 0	B	Help	Výsledek
161	V množině C řešte rovnici: (x + 1)⁴ = 81x⁴	A	Help	Výsledek
162	V množině C řešte rovnici s reálným parametem p: px² + 2(p - 1)x + p - 5 = 0	B	Help	Výsledek
163	V množině C řešte rovnici: (x³ - 1)² + (x³ + 1)² = 0	A	Help	Výsledek
164	V množině C řešte rovnici: (x⁴ + 1)² + 2(x⁴ + 1) - 8 = 0	A	Help	Výsledek
165	V množině C řešte rovnici: (x² + 4)(x² -i) = 0	B	Help	Výsledek
166	V množině C řešte rovnici:	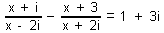A	Help	Výsledek
167	V množině C řešte rovnici:	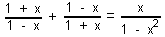B	Help	Výsledek
168	V množině C řešte rovnici: 16x⁴ = (x - 1)⁴	A	Help	Výsledek
169	V množině C řešte rovnici:	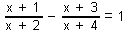B	Help	Výsledek
170	V množině C řešte rovnici: x² + 18 - 6i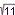 = 0	A	Help	Výsledek
171	Rozložte v C v součiny kvadratické trojčleny: x² - 2x + 1	B	Help	Výsledek
172	V množině C řešte rovnici: x² - 4 - i = 0	A	Help	Výsledek
173	Rozložte v C v součiny kvadratické trojčleny: x² + 4x + 13	B	Help	Výsledek
174	V množině C řešte rovnici: x² + 6 + 8i = 0	A	Help	Výsledek
175	Rozložte v C v součiny kvadratické trojčleny: x² - (-2 + i)x - 2i	A	Help	Výsledek
176	V množině C řešte soustavu rovnic: x + y = -i , x² + y² = 1	B	Help	Výsledek
177	Rozložte v C v součiny kvadratické trojčleny: x² + 5 + 12i	A	Help	Výsledek
178	V množině C řešte rovnici: x⁴ - 4x³+ 6x² - 4x = 80	A	Help	Výsledek
179	V množině C řešte soustavu rovnic: x + y = -i , x² + y² = -1	B	Help	Výsledek
180	V množině C řešte rovnici: x³ + 3x² + 3x = 7	A	Help	Výsledek
181	V množině C řešte rovnici: x⁴ - 2x³ + 3x² - 2x + 2 = 0 , víte-li, že má kořen x=i	A	Help	Výsledek

D. Kontrolní test

E.Náhodný test

F. Hodnocení výsledků a komunikace s učitelem (tutorem)

Vytisknout certifikat

Hodnocení výsledků:

Komunikace s učitelem (tutorem):

Tato část je určena pouze pro registrované uživatele. Zaregistrujte se!