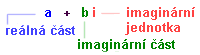Matika krokem - 1.lekce ...

Komplexní čísla
1.lekce - Definice, rovnost, sčítání, odčítání a násobení komplexních čísel
 Vytisknout  
Skype výuka, doučování
A. Výklad a ukázkové příklady

Definice

Každé komplexní číslo lze vyjádřit v algebraickém tvaru
a + bi
kde a , b jsou reálná čísla.

        Pro imaginární jednotku platí i2 = -1 		(1)

Rozdělení komplexních čísel lze znázornit takto:


Tato čísla nám umožňují odmocnit záporné číslo:
i2 = -1 tedy = i
(3i)2 = -9 tedy = 3i
(i)2 = -5 tedy = i
a tím i řešit kvadratickou rovnici se záporným diskriminantem.

Jak budeme s těmito čísly počítat?

Součet, rozdíl a součin

Součet , rozdíl , součin provádíme s těmito čísly stejně jako s dvojčleny s tím, že i2 = -1.

(2)

Příklad 1: Vypočtěte [3(2 - i)-(1 + i)]2
= Podle (2) platí:
[3(2 - i)-(1 + i)]2 = [6 - 3i - 1 - i]2 = (5 - 4i)2] = 25 - 40i + 16i2 = 25 - 40i - 16 = 9 - 40i
Výsledek:    9 - 40i


Mocnina imaginární jednotky

Pro přirozené mocniny i platí:   
i 4k = 1 ;      i 4k+1 = i ;      i 4k+2 = -1 ;      i 4k+3 = -i
(3)


Příklad 2: Vypočtěte i13 - i23 + i14 - i15 - i32
= i13 - i23 + i14 - i15 - i32 = i - (-i) + (-1) - (-i) - 1 = 3i - 2
Výsledek:    3i - 2


Rovnost

Dvě komplexní čísla se rovnají, rovnají-li se jejich části reálné i jejich části imaginární (4)


Příklad 3: Kdy bude číslo u = 3 - 2i rovno číslu v = p + qi?.
= Pokud číslo u = 3 - 2i má být rovno v = p + qi , musí platit p = 3 a současně q = -2


Příklad 4: Určete reálná čísla a,b tak, aby platilo: (2 - i)a - (-3 +i)b = 4 - 3i
= Nejdřív upravíme:
2a -ai + 3b -bi = 4 - 3i
2a + 3b + i(-a - b) = 4 - 3i
Nyní se musí rovnat reálné části obou čísel i imaginární části, tedy:
2a + 3b = 4    a současně    -a - b = -3
Řešením této soustavy (sčítací metodou) dostaneme:
2a + 3b =   4
 -a  -    b = -3       /.2
-----------------
b = -2    ,   a = 5
Výsledek:   a = 5    b = -2


Pravidla

V oboru komplexních čísel (označujeme C) můžeme bez omezení sčítat, odčítat a násobit (dělení až příště).
Pro počítání v C platí podobně jako v R:
Sčítání i násobení komplexních čísel je komutativní / a + b = b + a / a asociativní / a + ( b + c ) = ( a + b) + c /.
Násobení je distributivní vzhledem ke sčítání / a.( b + c ) = a.c + b.c /
Je-li součin dvou komplexníxh čísel roven nule, je rovno nule aspoň jedno z nich.
Pro mocniny komplexních čísel s přirozeným exponentem platí stejná pravidla jako pro mocniny čísel reálných:
zm . zn = zm + n
( x . z )m = xm . zm
( zm )n = zm.n

A teď je řada na tobě. Pochlub se, jak to umíš.
V části B ti ještě sem tam poradím, v Déčku už na to budeš jenom sám!


B. Příklady s krokovou kontrolou e-učitele

Příklad 1:    Vypočítejte: (2 - i)(3 - 2i)  -   3(1 - i)2=       


Příklad 2:    Určete reálná čísla x, y tak, aby platilo: (3 - 5i)x - (2 + i)y = -3i       


Příklad 3:    Vypočítejte: (i11 - i12 - i13 + i 14 ) . i11.i7.i5/ i16 =       



C. Příklady na procvičení učiva

 Na následujících příkladech s výsledky se můžete zdokonalit ve znalostech učiva této lekce.
 Pokud si nevíte s příkladem rady, užijte stručné nápovědy - Help.
Příklady označené A mají největší obtížnost, B střední a C nejmenší.

1Vypočtěte:  AHelp Výsledek
2Vypočtěte a výsledek zapište v algebraickém tvaru: (3 - i)(2 + 3i) + (1 - 4i)(2 - i)CHelp Výsledek
3Vypočtěte a výsledek zapište v algebraickém tvaru: (1 - i)2 - (1 + i)2BHelp Výsledek
4Vypočtěte a výsledek zapište v algebraickém tvaru: (1 - i)3 - (1 + i)3AHelp Výsledek
5Určete reálná čísla x, y, která jsou řešením rovnice: 4(2 + i)x + (1 - 4i)y + 7 = (3 + i)x - 6(2i - 1) + 9iBHelp Výsledek
6Vypočtěte a výsledek zapište v algebraickém tvaru: [(1 + 2i) - (4 + 3i)].(-i) - (4 + 3i)CHelp Výsledek
7Určete reálná čísla x, y, která jsou řešením rovnice: (x + y)(5 - 4i) + (x - y)(4 - 5i) = 94 - 68iBHelp Výsledek
8Vypočtěte a výsledek zapište v algebraickém tvaru: (-2 - 4i)(-0,5 + 0,5i) - (1 - 2i)CHelp Výsledek
9Vypočtěte: i3 + i13 + i33 + i43BHelp Výsledek
10Vypočtěte a výsledek zapište v algebraickém tvaru: [(-1 - 3i) - (-2 + i/2)].[((2 - i) - (1 - 2i)]CHelp Výsledek
11Vypočtěte: i + i2 + i3 + i4 + ... + i50BHelp Výsledek
12Vypočtěte: i + i4 + i8 + i12 + ... + i52CHelp Výsledek
13Vypočtěte: [(1+2i)-(3-i)](1-i)2BHelp Výsledek
14Vypočtěte: 3(-1+i)(1-i)-i(2-3i)CHelp Výsledek
15Vypočtěte: [(1+2i)-(3-i)]2(1-i)BHelp Výsledek
16Vypočtěte: (-i)i + (-i)iAHelp Výsledek
17Určete reálná čísla x, y tak, aby platilo: (1-i)x - (-2+i)y = 5 - 2iBHelp Výsledek
18Určete reálná čísla x, y tak, aby platilo: (+i)x - ()+i)y-1 = i2 - iAHelp Výsledek
19Vypočtěte:  (1 - 2i)(2 + 4i) - (3 + i)2BHelp Výsledek
20Vypočtěte co nejúsporněji:  (1 - i)12AHelp Výsledek
21Pro která reálná čísla x,y platí:  x(4 + i) + y(5 - 2i) = 2 + 7iBHelp Výsledek
22Vypočtěte co nejúsporněji:  (1 - i)6AHelp Výsledek
23Vypočtěte:  (8 - 5i)2BHelp Výsledek
24Vypočtěte:  AHelp Výsledek
25Vypočtěte:  (-3 + 4i)3BHelp Výsledek
26Vypočtěte co nejúsporněji:  (1 + i)8AHelp Výsledek
27Vypočtěte:  AHelp Výsledek
28Vypočtěte a výsledek zapište v algebraickém tvaru: (3 - i)(2 + 3i) + (1 - 4i)(2 - i)CHelp Výsledek
29Vypočtěte a výsledek zapište v algebraickém tvaru: (1 - i)2 - (1 + i)2BHelp Výsledek
30Vypočtěte a výsledek zapište v algebraickém tvaru: (1 - i)3 - (1 + i)3AHelp Výsledek
31Určete reálná čísla x, y, která jsou řešením rovnice: 4(2 + i)x + (1 - 4i)y + 7 = (3 + i)x - 6(2i - 1) + 9iBHelp Výsledek
32Vypočtěte a výsledek zapište v algebraickém tvaru: [(1 + 2i) - (4 + 3i)].(-i) - (4 + 3i)CHelp Výsledek
33Určete reálná čísla x, y, která jsou řešením rovnice: (x + y)(5 - 4i) + (x - y)(4 - 5i) = 94 - 68iBHelp Výsledek
34Vypočtěte a výsledek zapište v algebraickém tvaru: (-2 - 4i)(-0,5 + 0,5i) - (1 - 2i)CHelp Výsledek
35Vypočtěte: i3 + i13 + i33 + i43BHelp Výsledek
36Vypočtěte a výsledek zapište v algebraickém tvaru: [(-1 - 3i) - (-2 + i/2)].[((2 - i) - (1 - 2i)]CHelp Výsledek
37Vypočtěte: i + i2 + i3 + i4 + ... + i50BHelp Výsledek
38Vypočtěte: i + i4 + i8 + i12 + ... + i52CHelp Výsledek
39Vypočtěte: [(1+2i)-(3-i)](1-i)2BHelp Výsledek
40Vypočtěte: 3(-1+i)(1-i)-i(2-3i)CHelp Výsledek
41Vypočtěte: [(1+2i)-(3-i)]2(1-i)BHelp Výsledek
42Vypočtěte: (-i)i + (-i)iAHelp Výsledek
43Určete reálná čísla x, y tak, aby platilo: (1-i)x - (-2+i)y = 5 - 2iBHelp Výsledek
44Určete reálná čísla x, y tak, aby platilo: (+i)x - ()+i)y-1 = i2 - iAHelp Výsledek
45Vypočtěte:  (1 - 2i)(2 + 4i) - (3 + i)2BHelp Výsledek
46Vypočtěte co nejúsporněji:  (1 - i)12AHelp Výsledek
47Pro která reálná čísla x,y platí:  x(4 + i) + y(5 - 2i) = 2 + 7iBHelp Výsledek
48Vypočtěte co nejúsporněji:  (1 - i)6AHelp Výsledek
49Vypočtěte:  (8 - 5i)2BHelp Výsledek
50Vypočtěte:  AHelp Výsledek
51Vypočtěte:  (-3 + 4i)3BHelp Výsledek
52Vypočtěte co nejúsporněji:  (1 + i)8AHelp Výsledek


D. Kontrolní test

Vyzkoušejte si příklady, které jsou obměnou příkladů u maturity a přijímacích zkouškách na V© a otestujte svoji připravenost.


E.Náhodný test

Otestujte si znalost učiva této lekce na náhodně vybraných příkladech!


F. Hodnocení výsledků a komunikace s učitelem (tutorem)

Vytisknout certifikat

Hodnocení výsledků:

Komunikace s učitelem (tutorem):

Tato část je určena pouze pro registrované uživatele. Zaregistrujte se!