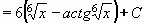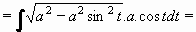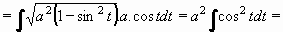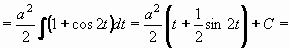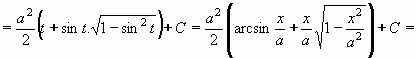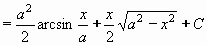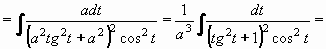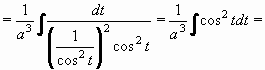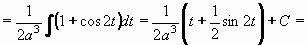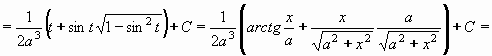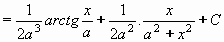| Matika krokem - 8.lekce ... |
|
Limita, derivace a integrál 8.lekce - Integrační metody - substituční metoda |
Vytisknout |
|||||||||||||||||||||||||||||||||||||
|
Skype výuka, doučování |
||||||||||||||||||||||||||||||||||||||
|
A. Výklad a ukázkové příklady
V dalších lekcích se budeme zabývat obtížnějšími partiemi, které pomůžou studentům s hlubším zájmem o matematiku nebo studentům VŠ. Výpočet neurčitých integrálů poskytuje hodně prostoru pro nápad a originální řešení. Zkusme tedy rozšířit dosud získané dovednosti. Nejprve musíme rozšířit pravidla integrování elementárních funkcí (Platí pro proměnné z definičního oboru výrazů):
Na příkladech si uvedená pravidla ukážeme: Příklad 70: Vypočtěte 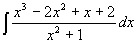
Příklad 71a: Vypočtěte 
Příklad 71b: Vypočtěte 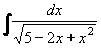
Poslední dva příklady demonstrují jak důležité je zapamatovat si nahoře uvedená pravidla (64) integrování elementárních funkcí! 1. Substituční metoda V 6.lekci jsme si ukázali substituční metodu, při které jsme používali pomocné proměnné t = g(x). V minulém příkladě to bylo t = 2x-4. Při výpočtu celé řady integrálů ale pomůžou i substituce jiného typu. Substituce x = g(t) Tato substituce často řeší integrály s odmocninami. Zvolíme za x takovou mocninu t, abychom se odmocnin zbavili. Příklad 72: Vypočtěte 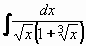
Goniometrická substituce x = a.sint , x = a.cost , x = a.tgt , x = a/tgt se hodí na integrály obsahující: 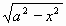 výraz se zjednoduší následným použitím vzorce ( 1-sin2t = cos2t ) výraz se zjednoduší následným použitím vzorce ( 1-sin2t = cos2t )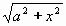 výraz se zjednoduší následným použitím vzorce ( 1+tg2t = 1/cos2t ) výraz se zjednoduší následným použitím vzorce ( 1+tg2t = 1/cos2t )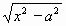 výraz se zjednoduší následným použitím vzorce ( 1/sin2t-1 = cotg2t ) výraz se zjednoduší následným použitím vzorce ( 1/sin2t-1 = cotg2t )
Příklad 73: Vypočtěte 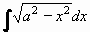
Příklad 74: Vypočtěte 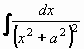
B. Příklady s krokovou kontrolou e-učitele C. Příklady na procvičení učiva Na následujících příkladech s výsledky se můžete zdokonalit ve znalostech učiva této lekce. Pokud si nevíte s příkladem rady, užijte stručné nápovědy - Help.
D. Kontrolní test E.Náhodný test F. Hodnocení výsledků a komunikace s učitelem (tutorem) Komunikace s učitelem (tutorem): Tato část je určena pouze pro registrované uživatele. Zaregistrujte se! |
||||||||||||||||||||||||||||||||||||||

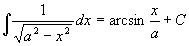
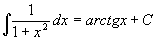
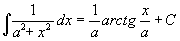
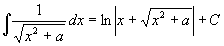
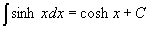
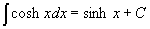
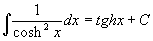
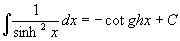
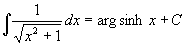
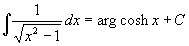
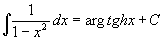
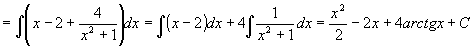


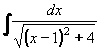 =
=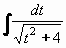 =
=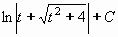 =
=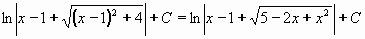
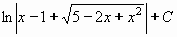
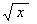 = t3 a
= t3 a
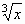 = t2.
= t2.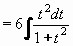
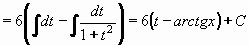
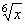 ) získáme konečný výsledek:
) získáme konečný výsledek: