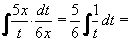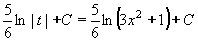A. Výklad a ukázkové příklady
Primitivní funkce
V předchozích lekcích jsme se naučili derivovat, kdy jsme z dané funkce hledali derivovanou funkci. Nyní se budeme zabývat
řešením úlohy v opačném směru, z derivované funkce určit funkci výchozí. Tato funkce se nejen v matematice
hledá velmi často a jmenuje se primitivní funkce.
Funkci F nazveme primitivní funkcí k funkci f v intervalu (a,b) jestliže F´(x) = f(x) pro všechna x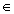 (a,b). (a,b).
| (42) |
|
Tak např. funkce F(x) = x5 je primitivní funkcí k funkci f = 5x4 v R,
protože v R platí: F´(x) = [x5]' = 5x4 = f(x).
Volně a nepřesně řečeno:
Primitivní funkcí k dané funkci je tedy funkce, kterou když zderivujeme, dostaneme danou funkci.
Příklad 49:
Najděte primitivní funkci F k funkci f: y = 3x2 - 2x v R.
| = |
Lze celkem snadno usoudit, že člen 3x2 vznikl derivací x3 a člen 2x derivací x2.
Primitivní funkcí tedy bude: F(x) = x3 - x2.
Snadno se vždy přesvědčíme o správnosti nalezené primitivní funkce derivováním. Derivací primitivní funkce musí být
funkce daná. To samozřejmě platí: F´(x) = [x3 - x2]´ = 3x2 - 2x.
Ale co kdyby někdo prohlásil, že primitivní funkcí k naší funkci f je také funkce G(x) = x3 - x2 + 1,
protože: G´(x) = [x3 - x2 + 1]´ = 3x2 - 2x = f(x).
Samozřejmě má pravdu. Navíc to platí nejen pro jedničku, ale pro jakoukoliv konstantu C, protože po zderivování "zmizí".
Množinou všech primitivních funkcí k funkci f: y = 3x2 - 2x je funkce F: y = x3 - x2 + C
|
Není tedy nalezení primitivní funkce (na rozdíl od derivování)
jednoznačný proces , ale platí:
|
Je-li funkce F primitivní funkcí k funkci f, pak každá další primitivní funkce k funkci f má tvar F(x) + C, kde C je reálná konstanta.
| (43) |
|
Neurčitý integrál
Nyní ještě zavedeme několik nových pojmů:
Operaci, kterou určujeme primitivní funkci F(x) + C k dané funkci f(x) nazýváme integrováním (inverzní operace k derivování).
Zápis úlohy intergrovat funkci f(x) provádíme: 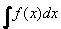 = F(x) + C, = F(x) + C,
kde se symbol 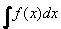 nazývá neurčitý integrál a představuje
množinu všech primitivních funkcí F(x) + C. nazývá neurčitý integrál a představuje
množinu všech primitivních funkcí F(x) + C.
 se nazývá integrační znak, f(x) integrand, dx diferenciál x, označuje integrační proměnnou a C je integrační konstanta. se nazývá integrační znak, f(x) integrand, dx diferenciál x, označuje integrační proměnnou a C je integrační konstanta.
| (44) |
|
Zadání předchozího příkladu č.49 ( Najděte primitivní funkci F k funkci f: y = 3x2 - 2x ) bychom mohli pomocí nových pojmů přeformulovat takto:
Integrujte funkci f: y = 3x2 - 2x. Zápis:  (3x2 - 2x)dx. (3x2 - 2x)dx.
Výsledek, který jsme získali ( Množina všech primitivních funkcí F je y = x3 - x2 + C ) zapíšeme:
 (3x2 - 2x)dx = x3 - x2 + C. (3x2 - 2x)dx = x3 - x2 + C.
Integrování funkcí
Z pravidel pro derivování elementárních funkcí (lekce 3) lze odvodit odpovídající pravidla integrování elementárních funkcí:
 a dx = ax + C , a je reálná konstanta a dx = ax + C , a je reálná konstanta
|
 xn dx = xn dx = 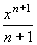 + C , n + C , n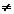 -1 -1
|
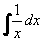 = ln|x| + C , x = ln|x| + C , x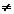 0 0
|
 ex dx = ex + C ex dx = ex + C
|
 ax dx = ax dx = 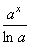 + C + C
|
 sinx dx = -cosx + C sinx dx = -cosx + C
|
 cosx dx = sinx + C cosx dx = sinx + C
|
 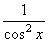 dx = tgx + C dx = tgx + C
|
 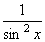 dx = -cotgx + C dx = -cotgx + C
|
|
| (45) |
|
Dále lze dokázat platnost věty o integraci součtu a rozdílu funkcí:
 c.f(x) dx = c c.f(x) dx = c  f(x) dx konstantu (v součinu) lze vyjmout před integrál f(x) dx konstantu (v součinu) lze vyjmout před integrál
 [f(x) + g(x)] dx = [f(x) + g(x)] dx =  f(x) dx + f(x) dx +  g(x) dx v součtu integrujeme jednotlivé sčítance g(x) dx v součtu integrujeme jednotlivé sčítance
 [f(x) - g(x)] dx = [f(x) - g(x)] dx =  f(x) dx - f(x) dx -  g(x) dx v rozdílu také integrujeme jednotlivé členy g(x) dx v rozdílu také integrujeme jednotlivé členy
Pozor! Neznáme pravidlo pro integraci součinu a integraci podílu funkcí.
| (46) |
|
Nyní si uvedená pravidla ukážeme na příkladech:
Příklad 50:
Vypočtěte  (x2 - 4x + 5) dx (x2 - 4x + 5) dx
| = |
Použijeme pravidla (46) a integrujeme člen po členu:
=  x2 dx - 4. x2 dx - 4. x dx + 5. x dx + 5. dx = dx =
Nyní použijeme pravidla (45) pro integraci elementárních funkcí:
= x3/3 - 4x2/2 + 5.x + C = x3/3 - 2x2 + 5x + C
|
Příklad 51:
Vypočtěte  (3ex -2sinx + 5) dx (3ex -2sinx + 5) dx
| = |
= 3 ex - 2 ex - 2 sinx dx + 5 sinx dx + 5 dx =
3ex - 2(-cosx) + 5x + C = 3ex + 2cosx + 5x + C dx =
3ex - 2(-cosx) + 5x + C = 3ex + 2cosx + 5x + C
|
V příkladech obsahujících součin popř. mocninu, nejprve provedeme příslušné operace a potom integrujeme člen po členu.
Příklad 52:
Vypočtěte  (x - 1)2(x + 2) dx (x - 1)2(x + 2) dx
| = |
Nejprve umocníme a vynásobíme:
=  (x2 - 2x + 1)(x + 2) dx = (x2 - 2x + 1)(x + 2) dx =
 (x3 - 2x2 + x + 2x2 - 4x + 2) dx = (x3 - 2x2 + x + 2x2 - 4x + 2) dx =
 (x3 - 3x + 2) dx = (x3 - 3x + 2) dx =
Nyní již integrujeme člen po členu:
= x4/4 - 3x2/2 + 2x + C
|
Obdobně postupujeme v příkladech obsahujících podíl.
Příklad 53:
Vypočtěte  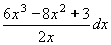
| = |
Nejprve zlomek rozložíme na dílčí zlomky a ty zjednodušíme (osdstraníme):
=  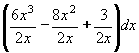 = =
 (3x2 - 4x + 1,5x-1) dx = (3x2 - 4x + 1,5x-1) dx =
A opět již integrujeme člen po členu:
= 3 x2 - 4 x2 - 4 x dx + 1,5 x dx + 1,5 x-1 + C =
3x3/3 - 4x2/2 + 1,5ln|x| + C = x3 - 2x2 + 1,5ln|x| + C x-1 + C =
3x3/3 - 4x2/2 + 1,5ln|x| + C = x3 - 2x2 + 1,5ln|x| + C
|
Odmocniny převádíme na mocniny s racionálním exponentem.
Příklad 54:
Vypočtěte 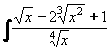 dx dx
| = |
Nejprve převedeme na mocniny s racionálním exponentem a rozdělíme na jednoduché zlomky:
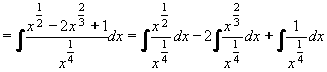
Zlomky odstraníme a integrujeme člen po členu:
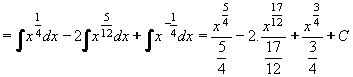
Nakonec převedeme zpět na odmocniny:
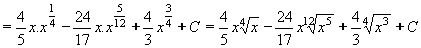
|
Na závěr příklad s geometrickou tematikou:
Příklad 55:
Určete křivku, která prochází bodem A[-4,5] a jejíž tečna v libovolném jejím bodě [x,y] má směrnici 2x + 4.
| = |
Směrnice tečny je dána derivací funkce a tedy ze směrnice dostaneme zpětně funkci integrací.
y =  (2x + 4) dx = x2 + 4x + C. (2x + 4) dx = x2 + 4x + C.
Integrační konstantu C určíme z podmínky, že má procházet bodem A - dosadíme:
5 = (-4)2 + 4(-4) + C a tedy C = 5
Hledaná křivka má rovnici: y = x2 + 4x + 5 a jedná se o parabolu.
Výsledek: Hledanou křivkou ja parabola y = x2 + 4x + 5
|
Pro výpočet integrálů složitějších funkcí slouží celá řada integračních metod. Uvedeme zde dvě nejdůležitější -
metodu per partes a metodu substituční.
Per partes
Metoda per partes - integrace po částech - vychází z derivace součinu funkcí:
(uv)´ = u´v + uv´
Odtud dostáváme:
uv =  u´v dx + u´v dx +  uv´dx uv´dx
Vyjádříme-li první integrál dostáváme výsledný vztah:
 u´v dx = uv - u´v dx = uv -  uv´dx uv´dx
| (47) |
|
Příklad 56:
Vypočtěte  x.cosx dx. x.cosx dx.
| = |
V metodě per partes výpočet integrálu na levé straně (47) nahrazujeme integrálem vpravo. Ten musíme umět samozřejmě
vypočítat.
Musíme tedy rozhodnout, jak dosadit do vztahu (47) za funkce u' a v, abychom si s integrálem vpravo poradili.
Zkusíme zvolit u´= x a v = cosx. Potom by platilo: u = x2/2 a v´= -sinx
Po dosazení do (47) by vzniklo:
 x.cosx dx = x2/2.cosx - x.cosx dx = x2/2.cosx -  x2/2.(-sinx) dx x2/2.(-sinx) dx
Tento integrál je ale ještě složitější než původní. Proto zvolíme obráceně:
u´ = cosx a v = x . Potom u = sinx a v´ = 1
Po dosazení vznikne:
 x.cosx dx = x.sinx - x.cosx dx = x.sinx -  1.sinx dx = 1.sinx dx =
Tento integrál snadno vypočteme a tím požadovaný, zadaný integrál:
= x.sinx - (-cosx) + C = x.sinx + cosx + C
Zkouška: F'(x) = [x.sinx + cosx + C]' = 1.sinx + x.cosx + (-sinx) = x.cosx = f(x) ... OK
Výsledek:  x.cosx dx = x.sinx + cosx + C x.cosx dx = x.sinx + cosx + C
|
V některých případech musíme metoda per partes opakovat několikrát.
Příklad 57:
Vypočtěte  x2.sinx dx. x2.sinx dx.
| = |
Podobně jako v předchozím příkladě zvolíme u´ = sinx a v = x2. Potom u = -cosx a v´ = 2x .
Po dosazení vznikne:
 x2.sinx dx = -x2.cosx + 2 x2.sinx dx = -x2.cosx + 2 x.cosx dx = x.cosx dx =
Na tento integrál použijeme per partes ještě jednou. Zvolíme u´ = cosx a v = x. Potom u = sinx a v´ = 1 a pokračujeme:
= -x2.cosx + 2(x.sinx -  sinx dx) = -x2.cosx + 2x.sinx + 2cosx + C sinx dx) = -x2.cosx + 2x.sinx + 2cosx + C
Výsledek:  x2.sinx dx = -x2.cosx + 2x.sinx + 2cosx + C x2.sinx dx = -x2.cosx + 2x.sinx + 2cosx + C
|
Někdy se zase při opakované aplikaci per partes objeví znovu původní integrál. Potom tento integrál ze vzniklé rovnice
prostě vyjádříme (jako neznámou ze vzorce).
Příklad 58:
Vypočtěte  ex.sinx dx. ex.sinx dx.
| = |
Zvolíme u´ = ex a v = sinx. Potom u = ex a v´ = cosx a dosadíme:
 ex.sinx dx = ex.sinx - ex.sinx dx = ex.sinx -  ex.cosx dx = ex.cosx dx =
Použijeme ještě jednou per partes. Zvolíme u´ = ex a v = cosx. Potom u = ex a v´ = -sinx a dosadíme:
= ex.sinx - (ex.cosx +  ex.sinx dx) , ale to je původní integrál. ex.sinx dx) , ale to je původní integrál.
Vznikla tedy rovnice:
 ex.sinx dx = ex.sinx - ex.cosx - ex.sinx dx = ex.sinx - ex.cosx -  ex.sinx dx , ex.sinx dx ,
ze které ho vyjádříme. Nejprve převedeme na jednu stranu, separujeme:
2  ex.sinx dx = ex.sinx - ex.cosx ex.sinx dx = ex.sinx - ex.cosx
A dostáváme tedy konečný výsledek:
 ex.sinx dx = ex/2.(sinx - cosx) + C ex.sinx dx = ex/2.(sinx - cosx) + C
Výsledek:  ex.sinx dx = ex/2.(sinx - cosx) + C ex.sinx dx = ex/2.(sinx - cosx) + C
|
Substituční metoda
Tato metoda umožňuje zavedením nové, pomocné proměnné převést integrovanou funkci na funkci, kterou lze integrovat snadněji.
Přesněji to můžeme formulovat takto: Složenou funkci f(g(x)) zavedením pomocné proměnné t = g(x) převedeme na funkci f(t) a
diferenciál dx vyjádříme pomocí diferenciálu dt. Vzniklý jednodušší integrál proměnné t vypočítáme a nakonec se opět vrátíme k původní
proměnné x.
 f(g(x)).g´(x) dx = f(g(x)).g´(x) dx =  f(t) dt , kde t = g(x) f(t) dt , kde t = g(x)
| (48) |
|
Na příkladech si ukážeme použití této metody.
Příklad 59:
Vypočtěte  (2x - 3)5 dx. (2x - 3)5 dx.
| = |
Zkusme zavést neznámou t = 2x - 3. Potom t´ = 2 .
Derivaci t´ můžeme zapsat také jako podíl diferenciálů t´ = dt/dx.
Tento zápis přesněji vyjadřuje co derivujeme (t) a podle jaké proměnné (x).
Tedy dt/dx = 2.
Z této rovnice můžeme vyjádřit dx = dt/2.
Potom již můžeme dosadit do původního integrálu:
 (2x - 3)5 dx = (2x - 3)5 dx =  t5 dt/2 =
1/2 t5 dt/2 =
1/2 t5 dt = t5 dt =
Tento integrál snadno vypočteme:
= 1/2.t6/6 = 1/12.t6 =
A nakonec se vrátíme zpět k proměnné x a přidáme integrační konstantu C:
= 1/12.(2x - 3)6 + C
Zkouška: [1/12.(2x - 3)6 + C]' = 6.1/12.(2x - 3)5.2 = (2x - 3) 5
Výsledek:  (2x - 3)5 dx = 1/12.(2x - 3)6 + C (2x - 3)5 dx = 1/12.(2x - 3)6 + C
|
Příklad 60:
Vypočtěte 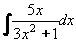
| = |
Zavedeme substituci t = 3x2 + 1. Potom t´ = 6x = dt/dx.
Z této rovnice vyjádřit 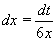 . .
Nyní již můžeme dosadit do původního integrálu:
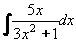 = = 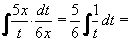
Po dosazení nové pomocné proměnné (t) musí původní proměnná (x) vždy zmizet!
(Jinak je tato substituce nepoužitelná a musíme volit jinak)
Tento integrál s proměnnou t snadno vypočteme a opět se vrátíme k proměnné x:
= 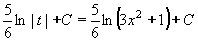
Absolutní hodnotu můžeme vynechat, protože je výraz 3x2 + 1 vždy kladný.
Výsledek: 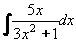 = 5/6.ln(3x2 + 1) + C = 5/6.ln(3x2 + 1) + C
|
B. Příklady s krokovou kontrolou e-učitele
C. Příklady na procvičení učiva
Na následujících příkladech s výsledky se můžete zdokonalit ve znalostech učiva této lekce.
Pokud si nevíte s příkladem rady, užijte stručné nápovědy - Help.
| Příklady označené | A mají největší obtížnost, | B střední a | C nejmenší. |
D. Kontrolní test
E.Náhodný test
F. Hodnocení výsledků a komunikace s učitelem (tutorem)
Vytisknout certifikat
Hodnocení výsledků:
Komunikace s učitelem (tutorem):
Tato část je určena pouze pro registrované uživatele. Zaregistrujte se!
|
 (3x2 - 2x)dx.
(3x2 - 2x)dx.  (3x2 - 2x)dx = x3 - x2 + C.
(3x2 - 2x)dx = x3 - x2 + C. (x2 - 4x + 5) dx
(x2 - 4x + 5) dx (3ex -2sinx + 5) dx
(3ex -2sinx + 5) dx (x - 1)2(x + 2) dx
(x - 1)2(x + 2) dx
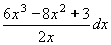
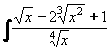 dx
dx u´v dx +
u´v dx +  uv´dx
uv´dx x.cosx dx.
x.cosx dx. x2.sinx dx.
x2.sinx dx. ex.sinx dx.
ex.sinx dx. (2x - 3)5 dx.
(2x - 3)5 dx.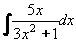
 (a,b).
(a,b).
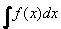 = F(x) + C,
= F(x) + C, 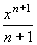 + C , n
+ C , n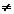 -1
-1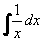 = ln|x| + C , x
= ln|x| + C , x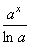 + C
+ C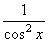 dx = tgx + C
dx = tgx + C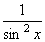 dx = -cotgx + C
dx = -cotgx + C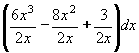 =
=
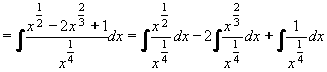
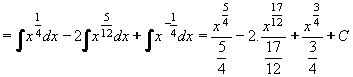
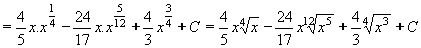
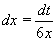 .
.