| Matika krokem - 4.lekce ... |
|
Limita, derivace a integrál 4.lekce - Průběh funkce |
Vytisknout |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
Skype výuka, doučování
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
A. Výklad a ukázkové příklady
Intervaly, ve kterých je funkce rostoucí nebo klesající, se nazývají intervaly monotónnosti. Jejich určení patří k základním požadavkům při zjišťování průběhu funkce. Intervaly monotónnosti funkce Derivace funkce v bodě xo definovaná jako  nám vlastně udává okamžitou změnu funkce f v tomto bodě.
Zvětší-li se hodnota proměnné x (Dx > 0) a hodnota funkce y se také zvětší (Dy > 0), je derivace v tomto bodě
kladná a funkce je rostoucí.Zvětší-li se hodnota proměnné x (Dx > 0) a hodnota funkce y se zmenší (Dy < 0), je derivace v tomto bodě záporná a funkce je klesající. Pokud se hodnota funkce se změnou hodnoty proměnné nemění (Dy = 0) , je derivace v tomto bodě rovna nule a funkce je konstantní. Z toho vyplývá následující souvislost derivace a monotónnosti funkce:
Příklad 33: Určete intervaly monotónnosti funkce f: y = x3 - 3x2.
Extrémy funkce 
Lokální extrémy funkce souhrnně označují maxima a minima dané funkce v určitém intervalu ("místně") - lokální maximum,
lokální minimum.Funkce f má v bodě xo [ostré] lokální maximum, jestliže existuje interval (a,b) tak, že pro všechna x z tohoto intervalu platí: [f(x) < f(xo)] f(x)  f(xo) Funkce f má v bodě xo [ostré] lokální minimum, jestliže existuje interval (a,b) tak, že pro všechna x z tohoto intervalu platí: [f(x) > f(xo)] f(x)  f(xo) Na vedlejším obrázku vidíme, že funkce f má lokální ostré maximum v bodě x1 a v bodě x3, lokální ostré minimum v bodě x2 a x4. Z obrázku je zřejmé, že v lokálních extrémech buď tečna (a tedy i derivace) neexistuje (bod x2) nebo je tečna rovnoběžná s osou x (x1, x3, x4) a derivace je tedy rovna rovna nule. Proto můžeme vyslovit nutnou podmínku existence extrému:
Proto při hledání lokálních extrémů funkce f(x) hledáme body x, pro které platí: f'(x) = 0. Tyto body jsou "podezřelé z extrému" a nazýváme je stacionární body. Zda má funkce v těchto bodech skutečně lokální extrém, rozhodne chování první derivace ve stacionárním bodě. 
 a) V bodě xo má funkce lokální maximum - Jestliže x se přibližuje k xo zleva, je funkce rostoucí a derivace kladná, v bodě xo je rovna nule a vpravo, za bodem xo je funkce klesající a derivace záporná. Znaménko derivace se tedy mění z plus na minus. b) V bodě xo má funkce lokální minimum - Jestliže x se přibližuje k xo zleva, je funkce klesající a derivace záporná, v bodě xo je rovna nule a vpravo, za bodem xo je funkce rostoucí a derivace kladná. Znaménko derivace se tedy mění z minus na plus. c) V bodě xo nemá funkce lokální extrém - Jestliže x se přibližuje k xo zleva, je funkce rostoucí a derivace kladná, v bodě xo je rovna nule a vpravo, za bodem xo je funkce opět rostoucí a derivace kladná. Znaménko derivace se tedy nemění. d) V bodě xo nemá funkce lokální extrém - Jestliže x se přibližuje k xo zleva, je funkce klesající a derivace záporná, v bodě xo je rovna nule a vpravo, za bodem xo je funkce opět klesající a derivace záporná. Znaménko derivace se tedy nemění.
Příklad 34: Vyšetřete lokální extrémy funkce f: y = x3 - 3x2.
V některých případech lze rozhodnout o existenci extrému ve stacionárním bodě xo pomocí 2.derivace (podmínkou je snadný výpočet 2.derivace a existence nenulové 2.derivace v tomto bodě). Je-li f''(xo) < 0 , má funkce v bodě xo ostré lokální maximum. Je-li f''(xo) > 0 , má funkce v bodě xo ostré lokální minimum. Je-li f''(xo) = 0 , nelze pomocí 2.derivace rozhodnout o existenci extrému. Globální extrémy (absolutní extrémy) funkce v nějakém intervalu představují body, ve kterých nabývá funkce své největší resp. nejmenší hodnoty. Znamená to nalézt lokální extrémy a porovnat odpovídající funkční hodnoty i s hodnotami v hraničních bodech intervalu. Největší hodnota přísluší globálnímu maximu a nejmenší globálnímu minimu.  Tak například funkce f na obrázku má v uzavřeném intervalu <a,b> globální maximum v bodě x=a }hodnota f(a) je největší hodnotou funkce v tomto intervalu) a globální minimum v bodě x=x1 (hodnota y1 je nejmenší hodnotou funkce v tomto intervalu). V otevřeném intervalu (a,b) však globální maximum nemá (neexistuje bod, ve kterém má funkce největší hodnotu - bod a tam nepatří) a globální monimum je opět x=x1. 
V případě, kdy funkce má v daném (libovolném) intervalu pouze jediný stacionární bod, není třeba porovnávat s hraničními body, je lokální extrém zároveň i globální extrém. Názorně to demonstrují horní dva obrázky. Příklad 35: Najděte globální extrémy funkce f: y = x3/3 - x2 - 3x v intervalu <-2,9>.
Konvexnost a konkávnost funkce K přesnějšímu nakreslení a popisu grafu grafu funkce pomůže zjištění, zda je funkce konvexní nebo konkávní.  
Názorně: Graf funkce f leží nad tečnou v bodě xo - funkci nazýváme konvexní (konvexní - exponent = nad), graf funkce g leží pod tečnou v bodě xo - funkci nazýváme konkávní. Nyní přesněji,matematicky. Říkáme, že funkce f je v bodě xo konvexní (konkávní), existuje-li interval obsahující bod xo takový, že pro všechny body z tohoto intervalu leží body grafu funkce f nad (pod tečnou sestrojenou v bodě xo. Je-li funkce konvexní (konkávní) v každém bodě intervalu, říkáme, že je konvexní (konkávní) v tomto intarvalu. Zda je funkce v intervalu konvexní či konkávní, rozhodneme podle 2.derivace funkce.
Příklad 36: Určete intervaly, v nichž je funkce f: y = x3 - 3x2 konvexní, konkávní.
Je funkce f na obrázku v bodě xo konvexní nebo konkávní? 
Vlevo od bodu xo je funkce konkávní a vpravo je konvexní. V bodě xo funkce výrazně mění svůj prúběh. Graf přechází z polohy "pod tečnou" do polohy "nad tečnou". Tento bod se nazývá inflexní bod funkce f. Samozřejmě, že to může být i obráceně - graf přechází z polohy "nad tečnou" do polohy "pod tečnou" Při hledání inflexních bodů funkce (obdobný postup jako při hledání extrémů) musíme nejprve nalézt body, ve kterých se mění funkce konvexní (f''(x) > 0) na konkávní (f''(x) < 0) nebo naopak (body "podezřelé na inflexi"). V nich zřejmě musí být f''(x) = 0 a to je podmínka nutná pro existenci inflexního bodu.
O tom, zda tento "podezřelý" bod je skutečně inflexní bod, rozhoduje opět znaménková změna tentokrát druhé derivace.
Příklad 37: Najděte inflexní body funkce f: y = x3 - 3x2.
Asymptota grafu funkce 
Při sestrojování grafu funkce pomůže nalezení přímky, ke které se graf funkce neustále přibližuje - asymtoty.Například graf funkce f:  na obrázku má dvě asymptoty - přímku p a osu y.
Vzdálenost grafu funkce f od přímky p se s rostoucím x zmenšuje, stejně tak se zmenšuje pro x klesající (záporné).Pro x blížící se zleva bodu x = 0 , se graf neomezeně blíží k záporné poloose y a pro x blíčící se zprava k bodu x = 0 se graf blíží ke kladné poloose y. Co to znamená obecně, matematicky? Z obrázku vyplývá, že pokud má být přímka p: y = ax + b asymptotou grafu funkce f: y = f(x) , musí se s rostoucí hdnotou x vzdálenost d = f(x) - (ax + b) neustále zmenšovat , být v limitě rovna 0. Můžeme tedy asymptotu formulovat takto:
Jak ale zjistit z rovnice funkce f: y = f(x) , zda asymptoty má nebo nemá? Z rovnice (20) lze odvodit vztah pro výpočet koeficientů a, b rovnice asymptoty. Stačí v rovnici pouužít větu o limitě operací a vyjádřit a takto:     a podobně vyjádříme i koeficient b: 
Pomocí vztahu (20) tedy získáme směrnicovou rovnici asymptoty grafu f. Ale nesmíme zapomenout na přímky rovnoběžné s osou y, které nemají směrnicovou rovnici a také mohou být asymptotami (viz úvodné příklad). V bodě x = 0 nebyla funkce f definována. Pro x blížící se k bodu x = 0 zleva se graf přibližoval k záporné poloose y , tedy funkce měla v bodě x = 0 nevlastní limitu -  . Pro x blížící se
k bodu x = 0 zprava se graf přibližoval ke kladné poloose y , tedy funkce měla nevlastní limitu +.Podmínka existence takovýchto asymptot vyplývá z předchozího příkladu a určuje ji následující věta:
Příklad 38: Určete asymptoty grafu funkce f: z úvodního příkladu.
Když jsme si vysvětlili základní poučky a metody pro zjišťování dílčích parametrů funkce, můžeme přistoupit k jejich komplexní aplikaci při vyšetřování průběhu funkcí, kdy nás kromě sestrojení grafu bude zajímat určení základních vlastností dané funkce. Pro zapamatování a ujednocení si postup shrneme do Desatera průběhu funkce:
Příklad 39: Vyšetřete průběh funkce f: y = 2x2e-x.
B. Příklady s krokovou kontrolou e-učitele C. Příklady na procvičení učiva Na následujících příkladech s výsledky se můžete zdokonalit ve znalostech učiva této lekce. Pokud si nevíte s příkladem rady, užijte stručné nápovědy - Help.
D. Kontrolní test E.Náhodný test F. Hodnocení výsledků a komunikace s učitelem (tutorem) Komunikace s učitelem (tutorem): Tato část je určena pouze pro registrované uživatele. Zaregistrujte se! |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
nebo 
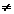f(x) .. funkce není sudá
a x = 2 + 
(Výpočet pomocí l'Hospitalova pravidla - viz.lekce 5.)
