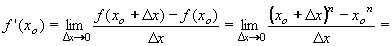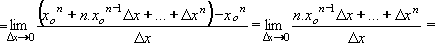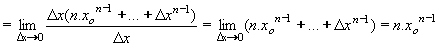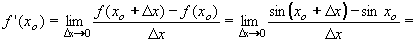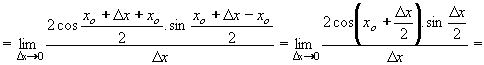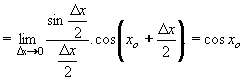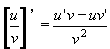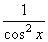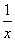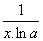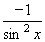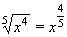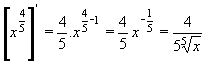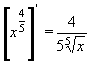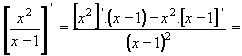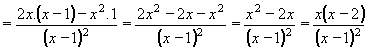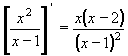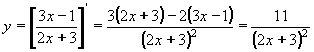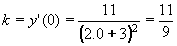| 1 | Vypočtěte derivaci funkce f: 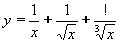 v libovol.bodě D(f) v libovol.bodě D(f) | C | Help |
Výsledek |
| 2 | Podle definice derivace vypočtěte derivaci funkce f: y = 2x2 - 3x + 1 | B | Help |
Výsledek |
| 3 | Podle definice derivace vypočtěte derivaci funkce f: y = x3 - 1 | B | Help |
Výsledek |
| 4 | Vypočtěte derivaci funkce f: 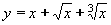 v libovol.bodě D(f) v libovol.bodě D(f) | C | Help |
Výsledek |
| 5 | Podle definice derivace vypočtěte derivaci funkce f: y = 3x - 2 | B | Help |
Výsledek |
| 6 | Podle definice derivace vypočtěte derivaci funkce f: y = (2x - 3)-1 | B | Help |
Výsledek |
| 7 | Vypočtěte derivaci funkce f: 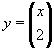 v libovol.bodě D(f) v libovol.bodě D(f) | C | Help |
Výsledek |
| 8 | Podle definice derivace vypočtěte derivaci funkce f: 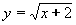 | B | Help |
Výsledek |
| 9 | Vypočtěte derivaci funkce f: 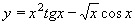 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 10 | Určete bod, ve kterém má graf funkce y = x.(1 + x)-1 tečnu procházející bodem M[3,?]. | A | Help |
Výsledek |
| 11 | Vypočtěte derivaci funkce f: 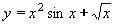 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 12 | Vypočtěte derivaci funkce f: 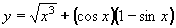 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 13 | Vypočtěte derivaci funkce f: 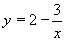 v libovol.bodě D(f) v libovol.bodě D(f) | C | Help |
Výsledek |
| 14 | Vypočtěte derivaci funkce f: 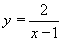 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 15 | Vypočtěte derivaci funkce f: 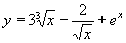 v libovol.bodě D(f) v libovol.bodě D(f) | C | Help |
Výsledek |
| 16 | Vypočtěte derivaci funkce f: 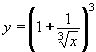 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 17 | Vypočtěte derivaci funkce f: 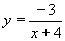 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 18 | Vypočtěte derivaci funkce f: 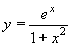 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 19 | Vypočtěte derivaci funkce f: 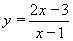 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 20 | Vypočtěte derivaci funkce f: 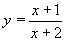 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 21 | Vypočtěte derivaci funkce f: 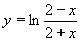 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 22 | Vypočtěte derivaci funkce f: 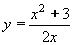 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 23 | Vypočtěte derivaci funkce f: 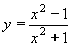 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 24 | Vypočtěte derivaci funkce f: y = xex(cosx + sinx) v libovol.bodě D(f) | A | Help |
Výsledek |
| 25 | Určete směrnici tečny grafu funkce f: y = sinx + cosx v jejím bodě T[p/6,?] | B | Help |
Výsledek |
| 26 | Určete směrnici tečny grafu funkce f: y = x.sinx v jejím bodě T[p/6,?] | B | Help |
Výsledek |
| 27 | Vypočtěte derivaci funkce f: 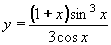 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 28 | Určete směrnici tečny grafu funkce f: 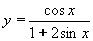 v jejím bodě T[p/6,?] v jejím bodě T[p/6,?] | B | Help |
Výsledek |
| 29 | Určete směrnici tečny grafu funkce f: y = x - tgx v jejím bodě T[p/3,?] | B | Help |
Výsledek |
| 30 | Vypočtěte derivaci funkce f: y = cosax.sinbx v libovol.bodě D(f) | A | Help |
Výsledek |
| 31 | Určete směrnici tečny grafu funkce f: y = 2sinx.cosx v jejím bodě T[p/6,?] | B | Help |
Výsledek |
| 32 | Určete směrnici tečny grafu funkce f: y = x2.cosx v jejím bodě T[p/3,?] | B | Help |
Výsledek |
| 33 | Vypočtěte derivaci funkce f: y = ln(1 - x2) v libovol.bodě D(f) | A | Help |
Výsledek |
| 34 | Vypočtěte derivaci funkce f: 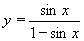 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 35 | Vypočtěte derivaci funkce f: 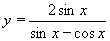 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 36 | Vypočtěte derivaci funkce f: 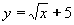 v libovol.bodě D(f) v libovol.bodě D(f) | C | Help |
Výsledek |
| 37 | Vypočtěte derivaci funkce f: 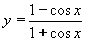 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 38 | Vypočtěte derivaci funkce f: 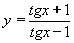 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 39 | Vypočtěte derivaci funkce f: 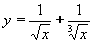 v libovol.bodě D(f) v libovol.bodě D(f) | C | Help |
Výsledek |
| 40 | Určete bod, ve kterém má graf funkce y = (2x + 1).x-1 tečnu, svírající s osou x úhel 45o. | B | Help |
Výsledek |
| 41 | Určete úhel, pod kterým protíná křivka y = x3 + x osu x. | C | Help |
Výsledek |
| 42 | Určete bod, ve kterém má graf funkce y = sinx - cosx tečnu, svírající s osou x úhel 45o. | B | Help |
Výsledek |
| 43 | Napište rovnici tečny a normály ke křivce o rovnici y = 8(4 + x2)-1 v bodě T[2,1]. | B | Help |
Výsledek |
| 44 | Napište rovnici tečny a normály ke křivce o rovnici y = 0,5x2 - 3x + 5 v bodě T[2,1]. | B | Help |
Výsledek |
| 45 | Určete úhel, pod kterým protíná křivka y = cosx osu x. | C | Help |
Výsledek |
| 46 | Napište rovnici tečny a normály ke křivce o rovnici y = 2x2 + 3x - 1 v bodě T[0,-1]. | B | Help |
Výsledek |
| 47 | Určete úhel, pod kterým protíná křivka y = 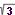 tgx osu x. tgx osu x. | C | Help |
Výsledek |
| 48 | Napište rovnici tečny a normály ke křivce o rovnici y = x3/3 - 5x - 4 v bodě T[-3,?]. | B | Help |
Výsledek |
| 49 | Určete bod, ve kterém má graf funkce y = 3x2 - 5x + 2 tečnu, svírající s osou x úhel 45o. | C | Help |
Výsledek |
| 50 | Napište rovnici tečny ke křivce o rovnici y = x2 - 5x + 6, je-li tečna rovnoběžná s přímkou y = x + 3 | B | Help |
Výsledek |
| 51 | Podle definice odvoďte okamžitou rychlost a zrychlení pohybu, jehož rovnice dráhy je s = at2. | B | Help |
Výsledek |
| 52 | Vypočtěte derivaci funkce f: 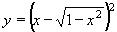 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 53 | Určete rychlost a zrychlení pohybu, jehož rovnice dráhy je: s = so + ct + 0,5gt2. | B | Help |
Výsledek |
| 54 | Vypočtěte derivaci funkce f: 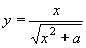 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 55 | Těleso o hmotnosti 10kg se pohybuje po přímce podle rovnice s = 1 + t + t2. Jakou kinetickou enerii (E=0,5mv2) bude mít toto těleso na konci páté sekundy (počítáme od t=0)? | B | Help |
Výsledek |
| 56 | Těleso se pohybuje nerovnoměrně podle rovnice s = 2t3 - 3. Určete jeho rychlost v metrech za sekundu po 10 sekundách pohybu (od t=0). | C | Help |
Výsledek |
| 57 | Vypočtěte derivaci funkce f: 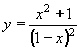 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 58 | Vypočtěte derivaci funkce f: y = (1 - x)3 v libovol.bodě D(f) | B | Help |
Výsledek |
| 59 | Vypočtěte derivaci funkce f: 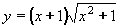 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 60 | Vypočtěte derivaci funkce f: y = (x3 - 2)5 v libovol.bodě D(f) | B | Help |
Výsledek |
| 61 | Vypočtěte derivaci funkce f: 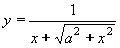 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 62 | Vypočtěte derivaci funkce f: y = (x4 - 6x2 + 7)3 v libovol.bodě D(f) | B | Help |
Výsledek |
| 63 | Vypočtěte derivaci funkce f: y = (x - 1)(x - 2)2(x - 3) v libovol.bodě D(f) | B | Help |
Výsledek |
| 64 | Vypočtěte derivaci funkce f: 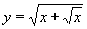 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 65 | Vypočtěte derivaci funkce f: y = (a2 - x2)-1 v libovol.bodě D(f) | B | Help |
Výsledek |
| 66 | Vypočtěte derivaci funkce f: 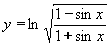 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 67 | Vypočtěte derivaci funkce f: y = (5 - x)-2 v libovol.bodě D(f) | B | Help |
Výsledek |
| 68 | Vypočtěte derivaci funkce f: 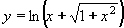 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 69 | Vypočtěte derivaci funkce f: 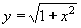 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 70 | Vypočtěte derivaci funkce f: 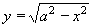 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 71 | Vypočtěte derivaci funkce f: 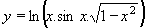 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 72 | Vypočtěte derivaci funkce f: 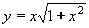 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 73 | Vypočtěte derivaci funkce f: y = (3x - 2)2(x + 1) v libovol.bodě D(f) | B | Help |
Výsledek |
| 74 | Vypočtěte derivaci funkce f: 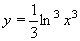 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 75 | Vypočtěte derivaci funkce f: y = (3x2 + 1)2 v libovol.bodě D(f) | B | Help |
Výsledek |
| 76 | Vypočtěte derivaci funkce f: y = (x2 - 2x + 2)3 v libovol.bodě D(f) | B | Help |
Výsledek |
| 77 | V rovnici paraboly y = x2 + bx + c určete hodnoty koeficientů b, c tak, aby se graf této funkce dotýkal přímky y = x v bodě x = 2. | A | Help |
Výsledek |
| 78 | Vypočtěte derivaci funkce f: y = 3cos2x - cos3x v libovol.bodě D(f) | B | Help |
Výsledek |
| 79 | Vypočtěte derivaci funkce f: 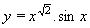 v libovol.bodě D(f) v libovol.bodě D(f) | C | Help |
Výsledek |
| 80 | Pod jakým úhlem protíná křivka y = lnx osu x? | B | Help |
Výsledek |
| 81 | Vypočtěte derivaci funkce f: 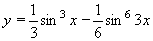 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 82 | Vypočtěte derivaci funkce f: 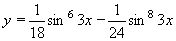 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 83 | Jaký vztah má platit mezi koeficienty p, q, aby se kubická parabola, jejíž rovnice je y = x3 + px + q, dotýkala osy x? | A | Help |
Výsledek |
| 84 | Pod jakym úhlem se protíná graf y = sinx a graf y = cosx | B | Help |
Výsledek |
| 85 | Vypočtěte derivaci funkce f: 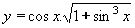 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 86 | Pod jakym úhlem se protíná parabola y = x2/2 a parabola 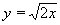 | B | Help |
Výsledek |
| 87 | Z bodu N[0,0] veďte tečny ke křivce y = x2 + 3x + 2. | A | Help |
Výsledek |
| 88 | Pod jakým úhlem se protíná hyperbola y = x-1 a parabola 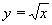 | B | Help |
Výsledek |
| 89 | Pod jakým úhlem se protíná graf y = x2 a graf x = y2 | B | Help |
Výsledek |
| 90 | Určete vzdálenost vrcholu paraboly y = x2 - 4x + 3 od tečny sestrojené v průsečíku této křivky s osou x. | A | Help |
Výsledek |
| 91 | Pod jakým úhlem se protíná graf y = cosx a graf y = 1/2 | B | Help |
Výsledek |
| 92 | Napište rovnici tečny paraboly y = 2 + x - x2 rovnoběžné s osou prvního kvadrantu. | B | Help |
Výsledek |
| 93 | Těleso sjede po nakloněné rovině 50 m dlouhé za 10 s. Předpokládáme-li, že dráha je kvadratickou funkcí času a že počáteční rychlost tělesa je rovna nule, jaká je jeho konečná rychlost? | A | Help |
Výsledek |
| 94 | Ve funkci y = x3 + 3x2 + cx + d určete koeficienty c, d tak, aby se daná křivka dotýkala osy prvního a třetího kvadrantu v bodě x = 2. | B | Help |
Výsledek |
| 95 | Podle definice derivace vypočtěte derivaci funkce f: y = x2-1 | B | Help |
Výsledek |
| 96 | Vlak se rozjíždí ze stanice pohybem vyjádřeným rovnicí s = at2 + bt + c a po uplynutí jedné minuty dosáhne rychlosti 60 km/h. Jak velkou vzálenost ujede, než této rychlosti dosáhne? Jaké je zrychlení onoho pohybu? | A | Help |
Výsledek |
| 97 | Podle definice derivace vypočtěte derivaci funkce f: y = x3-x | B | Help |
Výsledek |
| 98 | Rychlík jedoucí rychlostí 90 km/h má zabrzdit tak, aby se zastavil na vzdálenost 1 km. Po jaké době se zastaví,jestliže dráha vlaku při brzdění je kvadratickou funkcí času? Jaká bude jeho rychlost po 10 s od okamžiku, kdy začal brzdit? | A | Help |
Výsledek |
| 99 | Raketa se pohybuje po určitou krátkou dobu přímočaře podle rovnice s = (2/9).sin(pt/2) + so. Určete zrychlení tohoto pohybu na konci první sekundy (s je v metrech, t v sekundách). | B | Help |
Výsledek |
| 100 | Vypočtěte hodnotu derivace funkce y = x2 - 2x + 1 pro x = -2; -1; 0 | C | Help |
Výsledek |
| 101 | Podle definice derivace vypočtěte derivaci funkce f: y = x-1 | B | Help |
Výsledek |
| 102 | Podle definice derivace vypočtěte derivaci funkce f: y = (x + 2)2 | B | Help |
Výsledek |
| 103 | Z bodu M[-2,2] veďte tečny ke křivce y = x + x-1. | A | Help |
Výsledek |
| 104 | Podle definice derivace vypočtěte derivaci funkce f: y = (x + 3)/x | B | Help |
Výsledek |
| 105 | Vypočtěte hodnotu derivace funkce y = (x - 1).x-2 pro x = 1; 0; -1 | B | Help |
Výsledek |
| 106 | Ve které bodě paraboly y = x2 - 2x + 5 je nutno vést tečnu, aby byla kolmá k ose I. a III.kvadrantu? | B | Help |
Výsledek |
| 107 | Vypočtěte derivaci funkce f: y = (1 + nxm)(x + 1) v libovol.bodě D(f) | C | Help |
Výsledek |
| 108 | Vypočtěte hodnotu derivace funkce y = (x2 + 2x - 3).x-1 pro x = 2; -1; 4 | B | Help |
Výsledek |
| 109 | Vypočtěte hodnotu derivace funkce y = sinx.x-1 pro x = p/4 | B | Help |
Výsledek |
| 110 | Vypočtěte derivaci funkce f: 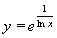 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 111 | Vypočtěte derivaci funkce f: y = (1 - x)(x + 2) v libovol.bodě D(f) | B | Help |
Výsledek |
| 112 | Vypočtěte derivaci funkce f: y = (1 - x2)(2 - x2) v libovol.bodě D(f) | B | Help |
Výsledek |
| 113 | Vypočtěte derivaci funkce f: y = 3x4 - 2x2 - 1 v libovol.bodě D(f) | C | Help |
Výsledek |
| 114 | Vypočtěte derivaci funkce f: y = sinx.cosx v libovol.bodě D(f) | B | Help |
Výsledek |
| 115 | Vypočtěte derivaci funkce f: 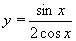 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 116 | Vypočtěte derivaci funkce f: y = 2x2 - 3x - 10 v libovol.bodě D(f) | C | Help |
Výsledek |
| 117 | Vypočtěte derivaci funkce f: 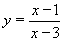 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 118 | Vypočtěte derivaci funkce f: 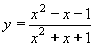 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 119 | Derivujte implicitní funkci f: x3 + ax2y + bxy2 + y3 = 0 | A | Help |
Výsledek |
| 120 | Vypočtěte derivaci funkce f: 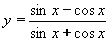 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 121 | Vypočtěte derivaci funkce f: 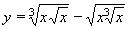 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 122 | Derivujte implicitní funkci f: x4 + y4 = x2y2 | A | Help |
Výsledek |
| 123 | Vypočtěte derivaci funkce f: 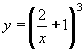 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 124 | Napište rovnici tečny křivky o rovnici x2 + y2 = 2 v bodě T[1,1]. | B | Help |
Výsledek |
| 125 | Derivujte implicitní funkci f: y2 - 2xy + b2 = 0 | A | Help |
Výsledek |
| 126 | Napište rovnici tečny křivky o rovnici x2 + y2 = 25 v bodě T[3,-4]. | B | Help |
Výsledek |
| 127 | Napište rovnici tečny křivky o rovnici 5x2 + y2 = 25 v bodě T[1,-2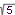 ]. ]. | B | Help |
Výsledek |
| 128 | Vypočtěte derivaci v bodě x=1 funkce f: 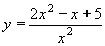 v libovol.bodě D(f) v libovol.bodě D(f) | C | Help |
Výsledek |
| 129 | Napište rovnici tečny křivky o rovnici y2 = 6x - 8 v bodě T[2,2]. | B | Help |
Výsledek |
| 130 | Derivujte implicitní funkci f: y3 - 3y + 2ax = 0 | B | Help |
Výsledek |
| 131 | Vypočtěte derivaci funkce f: 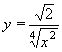 v libovol.bodě D(f) v libovol.bodě D(f) | C | Help |
Výsledek |
| 132 | Napište rovnici tečny křivky o rovnici x2 - 4y2 = 16 v bodě T[8,-2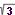 ]. ]. | B | Help |
Výsledek |
| 133 | Napište rovnici tečny křivky o rovnici 16x2 + 25y2 = 400 v bodě T[3,16/5 ]. | B | Help |
Výsledek |
| 134 | Najděte rovnici tečny grafu funkce f: y = ex - e-x v bodě T[0,?]. | B | Help |
Výsledek |
| 135 | Určete rovnici tečen ke křivce y = x3 + x2 - 6x v průsečících křivky s osou x. | A | Help |
Výsledek |
| 136 | Je dána parabola y = x2 - 4x + 3. Určete dotykový bod a rovnici tečny paraboly, která má směrový úhel 45o. | B | Help |
Výsledek |
| 137 | Je dána parabola y = x2 - 4x + 3. Pomocí derivace určete vrchol paraboly. | B | Help |
Výsledek |
| 138 | Je dána parabola y = 0,5x2 + 3x + 1. Určete rovnici tečny paraboly v bodě T[-2,?]. | B | Help |
Výsledek |
| 139 | Derivujte implicitní funkci f: y2cosx = a2.sin3x | A | Help |
Výsledek |
| 140 | Je dána parabola y = 0,5x2 + 3x + 1. Určete bod, ve kterém má parabola tečnu rovnoběžnou s přímkou 5x - y - 2 = 0. | B | Help |
Výsledek |
| 141 | Napište rovnici tečny křivky x2 + xy + y2 = 3 v bod2 T[-1,-1]. | B | Help |
Výsledek |
| 142 | Derivujte implicitní funkci f: x3 + y3 - 3axy = 0 | A | Help |
Výsledek |
| 143 | Vypočtěte derivaci funkce f: 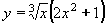 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 144 | Vypočtěte derivaci funkce f: 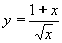 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 145 | Vypočtěte derivaci funkce f: y = log3(x2-sinx) v libovol.bodě D(f) | B | Help |
Výsledek |
| 146 | Derivujte implicitní funkci f: 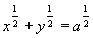 | A | Help |
Výsledek |
| 147 | Vypočtěte derivaci funkce f: 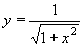 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 148 | Vypočtěte derivaci funkce f: 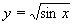 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 149 | Vypočtěte derivaci funkce f: 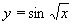 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 150 | Derivujte implicitní funkci f: 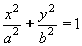 | A | Help |
Výsledek |
| 151 | Vypočtěte derivaci funkce f: 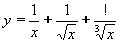 v libovol.bodě D(f) v libovol.bodě D(f) | C | Help |
Výsledek |
| 152 | Podle definice derivace vypočtěte derivaci funkce f: y = 2x2 - 3x + 1 | B | Help |
Výsledek |
| 153 | Podle definice derivace vypočtěte derivaci funkce f: y = x3 - 1 | B | Help |
Výsledek |
| 154 | Vypočtěte derivaci funkce f: 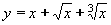 v libovol.bodě D(f) v libovol.bodě D(f) | C | Help |
Výsledek |
| 155 | Podle definice derivace vypočtěte derivaci funkce f: y = 3x - 2 | B | Help |
Výsledek |
| 156 | Podle definice derivace vypočtěte derivaci funkce f: y = (2x - 3)-1 | B | Help |
Výsledek |
| 157 | Vypočtěte derivaci funkce f: 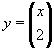 v libovol.bodě D(f) v libovol.bodě D(f) | C | Help |
Výsledek |
| 158 | Podle definice derivace vypočtěte derivaci funkce f: 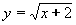 | B | Help |
Výsledek |
| 159 | Vypočtěte derivaci funkce f: 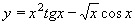 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 160 | Určete bod, ve kterém má graf funkce y = x.(1 + x)-1 tečnu procházející bodem M[3,?]. | A | Help |
Výsledek |
| 161 | Vypočtěte derivaci funkce f: 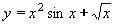 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 162 | Vypočtěte derivaci funkce f: 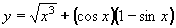 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 163 | Vypočtěte derivaci funkce f: 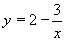 v libovol.bodě D(f) v libovol.bodě D(f) | C | Help |
Výsledek |
| 164 | Vypočtěte derivaci funkce f: 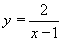 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 165 | Vypočtěte derivaci funkce f: 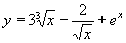 v libovol.bodě D(f) v libovol.bodě D(f) | C | Help |
Výsledek |
| 166 | Vypočtěte derivaci funkce f: 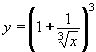 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 167 | Vypočtěte derivaci funkce f: 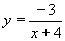 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 168 | Vypočtěte derivaci funkce f: 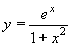 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 169 | Vypočtěte derivaci funkce f: 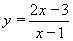 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 170 | Vypočtěte derivaci funkce f: 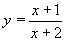 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 171 | Vypočtěte derivaci funkce f: 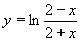 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 172 | Vypočtěte derivaci funkce f: 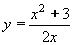 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 173 | Vypočtěte derivaci funkce f: 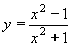 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 174 | Vypočtěte derivaci funkce f: y = xex(cosx + sinx) v libovol.bodě D(f) | A | Help |
Výsledek |
| 175 | Určete směrnici tečny grafu funkce f: y = sinx + cosx v jejím bodě T[p/6,?] | B | Help |
Výsledek |
| 176 | Určete směrnici tečny grafu funkce f: y = x.sinx v jejím bodě T[p/6,?] | B | Help |
Výsledek |
| 177 | Vypočtěte derivaci funkce f: 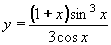 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 178 | Určete směrnici tečny grafu funkce f: 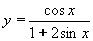 v jejím bodě T[p/6,?] v jejím bodě T[p/6,?] | B | Help |
Výsledek |
| 179 | Určete směrnici tečny grafu funkce f: y = x - tgx v jejím bodě T[p/3,?] | B | Help |
Výsledek |
| 180 | Vypočtěte derivaci funkce f: y = cosax.sinbx v libovol.bodě D(f) | A | Help |
Výsledek |
| 181 | Určete směrnici tečny grafu funkce f: y = 2sinx.cosx v jejím bodě T[p/6,?] | B | Help |
Výsledek |
| 182 | Určete směrnici tečny grafu funkce f: y = x2.cosx v jejím bodě T[p/3,?] | B | Help |
Výsledek |
| 183 | Vypočtěte derivaci funkce f: y = ln(1 - x2) v libovol.bodě D(f) | A | Help |
Výsledek |
| 184 | Vypočtěte derivaci funkce f: 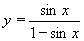 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 185 | Vypočtěte derivaci funkce f: 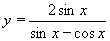 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 186 | Vypočtěte derivaci funkce f: 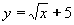 v libovol.bodě D(f) v libovol.bodě D(f) | C | Help |
Výsledek |
| 187 | Vypočtěte derivaci funkce f: 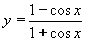 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 188 | Vypočtěte derivaci funkce f: 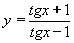 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 189 | Vypočtěte derivaci funkce f: 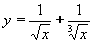 v libovol.bodě D(f) v libovol.bodě D(f) | C | Help |
Výsledek |
| 190 | Určete bod, ve kterém má graf funkce y = (2x + 1).x-1 tečnu, svírající s osou x úhel 45o. | B | Help |
Výsledek |
| 191 | Určete úhel, pod kterým protíná křivka y = x3 + x osu x. | C | Help |
Výsledek |
| 192 | Určete bod, ve kterém má graf funkce y = sinx - cosx tečnu, svírající s osou x úhel 45o. | B | Help |
Výsledek |
| 193 | Napište rovnici tečny a normály ke křivce o rovnici y = 8(4 + x2)-1 v bodě T[2,1]. | B | Help |
Výsledek |
| 194 | Napište rovnici tečny a normály ke křivce o rovnici y = 0,5x2 - 3x + 5 v bodě T[2,1]. | B | Help |
Výsledek |
| 195 | Určete úhel, pod kterým protíná křivka y = cosx osu x. | C | Help |
Výsledek |
| 196 | Napište rovnici tečny a normály ke křivce o rovnici y = 2x2 + 3x - 1 v bodě T[0,-1]. | B | Help |
Výsledek |
| 197 | Určete úhel, pod kterým protíná křivka y = 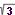 tgx osu x. tgx osu x. | C | Help |
Výsledek |
| 198 | Napište rovnici tečny a normály ke křivce o rovnici y = x3/3 - 5x - 4 v bodě T[-3,?]. | B | Help |
Výsledek |
| 199 | Určete bod, ve kterém má graf funkce y = 3x2 - 5x + 2 tečnu, svírající s osou x úhel 45o. | C | Help |
Výsledek |
| 200 | Napište rovnici tečny ke křivce o rovnici y = x2 - 5x + 6, je-li tečna rovnoběžná s přímkou y = x + 3 | B | Help |
Výsledek |
| 201 | Podle definice odvoďte okamžitou rychlost a zrychlení pohybu, jehož rovnice dráhy je s = at2. | B | Help |
Výsledek |
| 202 | Vypočtěte derivaci funkce f: 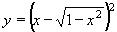 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 203 | Určete rychlost a zrychlení pohybu, jehož rovnice dráhy je: s = so + ct + 0,5gt2. | B | Help |
Výsledek |
| 204 | Vypočtěte derivaci funkce f: 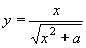 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 205 | Těleso o hmotnosti 10kg se pohybuje po přímce podle rovnice s = 1 + t + t2. Jakou kinetickou enerii (E=0,5mv2) bude mít toto těleso na konci páté sekundy (počítáme od t=0)? | B | Help |
Výsledek |
| 206 | Těleso se pohybuje nerovnoměrně podle rovnice s = 2t3 - 3. Určete jeho rychlost v metrech za sekundu po 10 sekundách pohybu (od t=0). | C | Help |
Výsledek |
| 207 | Vypočtěte derivaci funkce f: 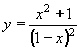 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 208 | Vypočtěte derivaci funkce f: y = (1 - x)3 v libovol.bodě D(f) | B | Help |
Výsledek |
| 209 | Vypočtěte derivaci funkce f: 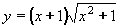 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 210 | Vypočtěte derivaci funkce f: y = (x3 - 2)5 v libovol.bodě D(f) | B | Help |
Výsledek |
| 211 | Vypočtěte derivaci funkce f: 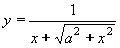 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 212 | Vypočtěte derivaci funkce f: y = (x4 - 6x2 + 7)3 v libovol.bodě D(f) | B | Help |
Výsledek |
| 213 | Vypočtěte derivaci funkce f: y = (x - 1)(x - 2)2(x - 3) v libovol.bodě D(f) | B | Help |
Výsledek |
| 214 | Vypočtěte derivaci funkce f: 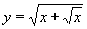 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 215 | Vypočtěte derivaci funkce f: y = (a2 - x2)-1 v libovol.bodě D(f) | B | Help |
Výsledek |
| 216 | Vypočtěte derivaci funkce f: 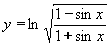 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 217 | Vypočtěte derivaci funkce f: y = (5 - x)-2 v libovol.bodě D(f) | B | Help |
Výsledek |
| 218 | Vypočtěte derivaci funkce f: 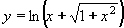 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 219 | Vypočtěte derivaci funkce f: 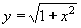 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 220 | Vypočtěte derivaci funkce f: 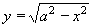 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 221 | Vypočtěte derivaci funkce f: 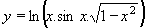 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 222 | Vypočtěte derivaci funkce f: 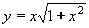 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 223 | Vypočtěte derivaci funkce f: y = (3x - 2)2(x + 1) v libovol.bodě D(f) | B | Help |
Výsledek |
| 224 | Vypočtěte derivaci funkce f: 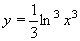 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 225 | Vypočtěte derivaci funkce f: y = (3x2 + 1)2 v libovol.bodě D(f) | B | Help |
Výsledek |
| 226 | Vypočtěte derivaci funkce f: y = (x2 - 2x + 2)3 v libovol.bodě D(f) | B | Help |
Výsledek |
| 227 | V rovnici paraboly y = x2 + bx + c určete hodnoty koeficientů b, c tak, aby se graf této funkce dotýkal přímky y = x v bodě x = 2. | A | Help |
Výsledek |
| 228 | Vypočtěte derivaci funkce f: y = 3cos2x - cos3x v libovol.bodě D(f) | B | Help |
Výsledek |
| 229 | Vypočtěte derivaci funkce f: 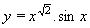 v libovol.bodě D(f) v libovol.bodě D(f) | C | Help |
Výsledek |
| 230 | Pod jakým úhlem protíná křivka y = lnx osu x? | B | Help |
Výsledek |
| 231 | Vypočtěte derivaci funkce f: 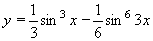 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 232 | Vypočtěte derivaci funkce f: 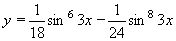 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 233 | Jaký vztah má platit mezi koeficienty p, q, aby se kubická parabola, jejíž rovnice je y = x3 + px + q, dotýkala osy x? | A | Help |
Výsledek |
| 234 | Pod jakym úhlem se protíná graf y = sinx a graf y = cosx | B | Help |
Výsledek |
| 235 | Vypočtěte derivaci funkce f: 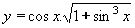 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 236 | Pod jakym úhlem se protíná parabola y = x2/2 a parabola 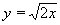 | B | Help |
Výsledek |
| 237 | Z bodu N[0,0] veďte tečny ke křivce y = x2 + 3x + 2. | A | Help |
Výsledek |
| 238 | Pod jakým úhlem se protíná hyperbola y = x-1 a parabola 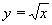 | B | Help |
Výsledek |
| 239 | Pod jakým úhlem se protíná graf y = x2 a graf x = y2 | B | Help |
Výsledek |
| 240 | Určete vzdálenost vrcholu paraboly y = x2 - 4x + 3 od tečny sestrojené v průsečíku této křivky s osou x. | A | Help |
Výsledek |
| 241 | Pod jakým úhlem se protíná graf y = cosx a graf y = 1/2 | B | Help |
Výsledek |
| 242 | Napište rovnici tečny paraboly y = 2 + x - x2 rovnoběžné s osou prvního kvadrantu. | B | Help |
Výsledek |
| 243 | Těleso sjede po nakloněné rovině 50 m dlouhé za 10 s. Předpokládáme-li, že dráha je kvadratickou funkcí času a že počáteční rychlost tělesa je rovna nule, jaká je jeho konečná rychlost? | A | Help |
Výsledek |
| 244 | Ve funkci y = x3 + 3x2 + cx + d určete koeficienty c, d tak, aby se daná křivka dotýkala osy prvního a třetího kvadrantu v bodě x = 2. | B | Help |
Výsledek |
| 245 | Podle definice derivace vypočtěte derivaci funkce f: y = x2-1 | B | Help |
Výsledek |
| 246 | Vlak se rozjíždí ze stanice pohybem vyjádřeným rovnicí s = at2 + bt + c a po uplynutí jedné minuty dosáhne rychlosti 60 km/h. Jak velkou vzálenost ujede, než této rychlosti dosáhne? Jaké je zrychlení onoho pohybu? | A | Help |
Výsledek |
| 247 | Podle definice derivace vypočtěte derivaci funkce f: y = x3-x | B | Help |
Výsledek |
| 248 | Rychlík jedoucí rychlostí 90 km/h má zabrzdit tak, aby se zastavil na vzdálenost 1 km. Po jaké době se zastaví,jestliže dráha vlaku při brzdění je kvadratickou funkcí času? Jaká bude jeho rychlost po 10 s od okamžiku, kdy začal brzdit? | A | Help |
Výsledek |
| 249 | Raketa se pohybuje po určitou krátkou dobu přímočaře podle rovnice s = (2/9).sin(pt/2) + so. Určete zrychlení tohoto pohybu na konci první sekundy (s je v metrech, t v sekundách). | B | Help |
Výsledek |
| 250 | Vypočtěte hodnotu derivace funkce y = x2 - 2x + 1 pro x = -2; -1; 0 | C | Help |
Výsledek |
| 251 | Podle definice derivace vypočtěte derivaci funkce f: y = x-1 | B | Help |
Výsledek |
| 252 | Podle definice derivace vypočtěte derivaci funkce f: y = (x + 2)2 | B | Help |
Výsledek |
| 253 | Z bodu M[-2,2] veďte tečny ke křivce y = x + x-1. | A | Help |
Výsledek |
| 254 | Podle definice derivace vypočtěte derivaci funkce f: y = (x + 3)/x | B | Help |
Výsledek |
| 255 | Vypočtěte hodnotu derivace funkce y = (x - 1).x-2 pro x = 1; 0; -1 | B | Help |
Výsledek |
| 256 | Ve které bodě paraboly y = x2 - 2x + 5 je nutno vést tečnu, aby byla kolmá k ose I. a III.kvadrantu? | B | Help |
Výsledek |
| 257 | Vypočtěte derivaci funkce f: y = (1 + nxm)(x + 1) v libovol.bodě D(f) | C | Help |
Výsledek |
| 258 | Vypočtěte hodnotu derivace funkce y = (x2 + 2x - 3).x-1 pro x = 2; -1; 4 | B | Help |
Výsledek |
| 259 | Vypočtěte hodnotu derivace funkce y = sinx.x-1 pro x = p/4 | B | Help |
Výsledek |
| 260 | Vypočtěte derivaci funkce f: 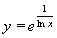 v libovol.bodě D(f) v libovol.bodě D(f) | A | Help |
Výsledek |
| 261 | Vypočtěte derivaci funkce f: y = (1 - x)(x + 2) v libovol.bodě D(f) | B | Help |
Výsledek |
| 262 | Vypočtěte derivaci funkce f: y = (1 - x2)(2 - x2) v libovol.bodě D(f) | B | Help |
Výsledek |
| 263 | Vypočtěte derivaci funkce f: y = 3x4 - 2x2 - 1 v libovol.bodě D(f) | C | Help |
Výsledek |
| 264 | Vypočtěte derivaci funkce f: y = sinx.cosx v libovol.bodě D(f) | B | Help |
Výsledek |
| 265 | Vypočtěte derivaci funkce f: 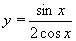 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 266 | Vypočtěte derivaci funkce f: y = 2x2 - 3x - 10 v libovol.bodě D(f) | C | Help |
Výsledek |
| 267 | Vypočtěte derivaci funkce f: 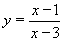 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 268 | Vypočtěte derivaci funkce f: 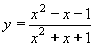 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 269 | Derivujte implicitní funkci f: x3 + ax2y + bxy2 + y3 = 0 | A | Help |
Výsledek |
| 270 | Vypočtěte derivaci funkce f: 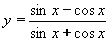 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 271 | Vypočtěte derivaci funkce f: 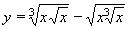 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 272 | Derivujte implicitní funkci f: x4 + y4 = x2y2 | A | Help |
Výsledek |
| 273 | Vypočtěte derivaci funkce f: 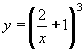 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 274 | Napište rovnici tečny křivky o rovnici x2 + y2 = 2 v bodě T[1,1]. | B | Help |
Výsledek |
| 275 | Derivujte implicitní funkci f: y2 - 2xy + b2 = 0 | A | Help |
Výsledek |
| 276 | Napište rovnici tečny křivky o rovnici x2 + y2 = 25 v bodě T[3,-4]. | B | Help |
Výsledek |
| 277 | Napište rovnici tečny křivky o rovnici 5x2 + y2 = 25 v bodě T[1,-2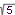 ]. ]. | B | Help |
Výsledek |
| 278 | Vypočtěte derivaci v bodě x=1 funkce f: 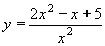 v libovol.bodě D(f) v libovol.bodě D(f) | C | Help |
Výsledek |
| 279 | Napište rovnici tečny křivky o rovnici y2 = 6x - 8 v bodě T[2,2]. | B | Help |
Výsledek |
| 280 | Derivujte implicitní funkci f: y3 - 3y + 2ax = 0 | B | Help |
Výsledek |
| 281 | Vypočtěte derivaci funkce f: 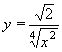 v libovol.bodě D(f) v libovol.bodě D(f) | C | Help |
Výsledek |
| 282 | Napište rovnici tečny křivky o rovnici x2 - 4y2 = 16 v bodě T[8,-2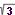 ]. ]. | B | Help |
Výsledek |
| 283 | Napište rovnici tečny křivky o rovnici 16x2 + 25y2 = 400 v bodě T[3,16/5 ]. | B | Help |
Výsledek |
| 284 | Najděte rovnici tečny grafu funkce f: y = ex - e-x v bodě T[0,?]. | B | Help |
Výsledek |
| 285 | Určete rovnici tečen ke křivce y = x3 + x2 - 6x v průsečících křivky s osou x. | A | Help |
Výsledek |
| 286 | Je dána parabola y = x2 - 4x + 3. Určete dotykový bod a rovnici tečny paraboly, která má směrový úhel 45o. | B | Help |
Výsledek |
| 287 | Je dána parabola y = x2 - 4x + 3. Pomocí derivace určete vrchol paraboly. | B | Help |
Výsledek |
| 288 | Je dána parabola y = 0,5x2 + 3x + 1. Určete rovnici tečny paraboly v bodě T[-2,?]. | B | Help |
Výsledek |
| 289 | Derivujte implicitní funkci f: y2cosx = a2.sin3x | A | Help |
Výsledek |
| 290 | Je dána parabola y = 0,5x2 + 3x + 1. Určete bod, ve kterém má parabola tečnu rovnoběžnou s přímkou 5x - y - 2 = 0. | B | Help |
Výsledek |
| 291 | Napište rovnici tečny křivky x2 + xy + y2 = 3 v bod2 T[-1,-1]. | B | Help |
Výsledek |
| 292 | Derivujte implicitní funkci f: x3 + y3 - 3axy = 0 | A | Help |
Výsledek |
| 293 | Vypočtěte derivaci funkce f: 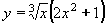 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 294 | Vypočtěte derivaci funkce f: 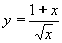 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 295 | Vypočtěte derivaci funkce f: y = log3(x2-sinx) v libovol.bodě D(f) | B | Help |
Výsledek |
| 296 | Derivujte implicitní funkci f: 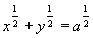 | A | Help |
Výsledek |
| 297 | Vypočtěte derivaci funkce f: 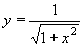 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 298 | Vypočtěte derivaci funkce f: 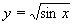 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 299 | Vypočtěte derivaci funkce f: 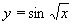 v libovol.bodě D(f) v libovol.bodě D(f) | B | Help |
Výsledek |
| 300 | Derivujte implicitní funkci f: 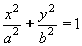 | A | Help |
Výsledek |
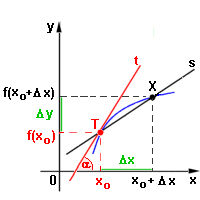 Derivace funkce
Derivace funkce
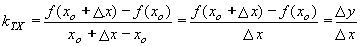 .
.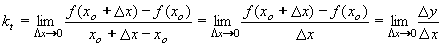 .
.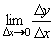 - má svůj vlastní název - derivace funkce.
- má svůj vlastní název - derivace funkce.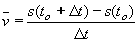
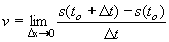
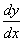 .
.
 ,
, ).
).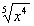 v libovolném bodě def.oboru.
v libovolném bodě def.oboru.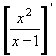 v libovolném bodě def.oboru.
v libovolném bodě def.oboru.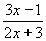 v bodě T[0,-1/3]
v bodě T[0,-1/3]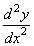 .
.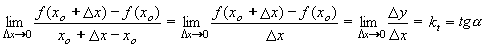
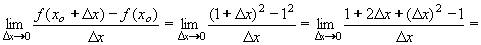
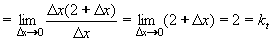
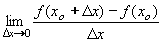
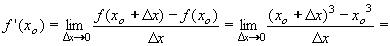
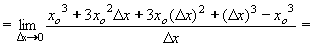
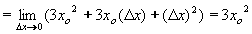
 R
R