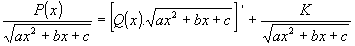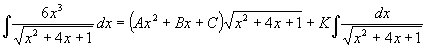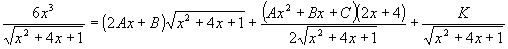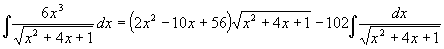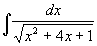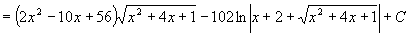A. Výklad a ukázkové příklady
Integrování iracionálních funkcí
Některé typy iracionálních funkcí lze vhodnými substitucemi převest na racionální funkce
a ty potom integrovat tak, jak jsme si ukázali v předchozí kapitole.
Integrály typu: 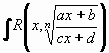 lze substitucí:
lze substitucí: 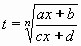 převést na integrály racionálních funkcí.
převést na integrály racionálních funkcí.
|
Příklad 83:
Vypočtěte 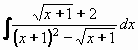
| = |
Zavedeme pomocnou neznámoiu
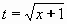 , ,
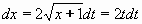
t2 = x + 1 , (x + 1)2 = t4
Po substituci vznikne integrál:
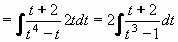
Toto je již racionální ryze lomená funkce, kterou integrujeme rozkladem na parciální zlomky:
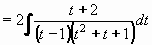
Metodou neurčitých koeficientů provedeme rozklad:
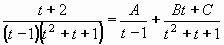
t + 2 = At2 + At + A + Bt2 - Bt + Ct - C
A + B = 0 , A - B + C = 1 , A - C = 2
A = 1 , B = -1 , C = -1
Pokračujeme integrováním parciálních zlomků:
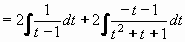
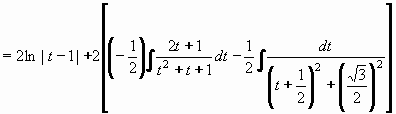
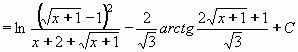
Po návratu k původní proměnné x dostáváme konečný výsledek.
Výsledek: 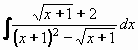 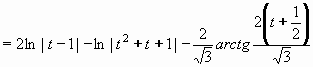
|
Integrace iracionálních funkcí typu 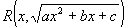 - Eulerovy substituce - Eulerovy substituce
Integrál typu 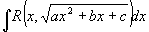 lze vždy racionalizovat (převést na integrál racionální funkce) pomocí některé ze tří Eulerových substitucí. lze vždy racionalizovat (převést na integrál racionální funkce) pomocí některé ze tří Eulerových substitucí.
1.Eulerova substituce - je použitelná pro a>0
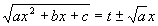
|
Použití této substituce si ukážeme na příkladě:
Příklad 84:
Vypočtěte 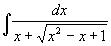
| = |
Protože a = 1 > 0 , položíme
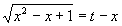
(znaménko +- vybíráme podle výhodnosti, pro - se zruší x)
Umocněním a úpravami vyjádříme x:
x2-x+1 = t2-2tx+x2
x(2t-1) = t2-1
x = (t2-1)/(2t-1)
Difernciál x získáme derivováním:
dx = 2(t2-t+1)dt/(2t-1)2
Po dosazení do původního integrálu:
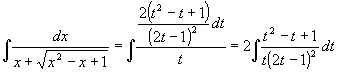
Rozkladem na parciální zlomky dostaneme:
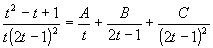
Po výpočtu A=1 , B=-3/2 , C=3/2 (např. metodou neurčitých součinitelů) pokračujeme:
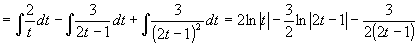
Nejprve z rovnice:
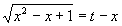
vyjádříme t:
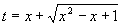
Dosazením za t se vrátíme k původní proměnné x a máme konečný výsledek:
Výsledek:
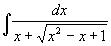 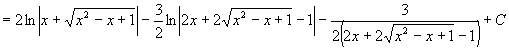
|
2.Eulerova substituce - je použitelná pro c>0
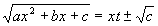
|
Použití této substituce si ukážeme na příkladě:
Příklad 85:
Vypočtěte 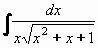
| = |
Protože c = 1 > 0 , položíme
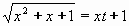
Umocněním a úpravami vyjádříme x:
x2+x+1 = x2t2+2tx+1
x2(1-t2) =x(2t-1)
x = (2t-1)/(1-t2)
Difernciál x získáme derivováním:
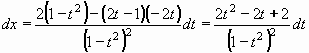
Vyjádříme také odmocninu:
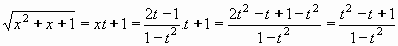
Po dosazení do původního integrálu:
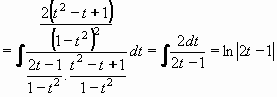
Z rovnice :
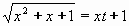
vyjádříme t:
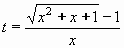
Návratem k původní proměnné x dostáváme:
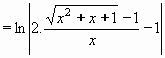 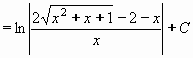
Výsledek: 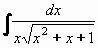 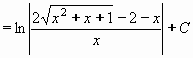
|
3.Eulerova substituce - má-li kvadratický trojčlen dva různé, reálné kořeny r, s: ax2 + bx + c = a(x - r)(x - s)
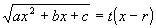
|
Použití této substituce si ukážeme na příkladě:
Příklad 86:
Vypočtěte 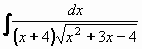
| = |
Kvadratický trojčlen lze rozložit: x2+3x-4=(x-1)(x+4)
Můžeme tedy použít substituci:
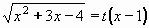
Umocněním a úpravami vyjádříme x:
x2+3x-4 = t2(x-1)2
t2=[(x-1)(x+4)]/[(x-1)(x-1)]=(x+4)/(x-1)
t2x-t2=x+4
x(t2-1)=t2+4
x=(t2+4)/(t2-1)
Difernciál x získáme derivováním:
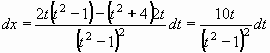
Vyjádříme také odmocninu:
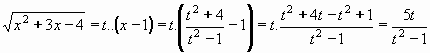
Po dosazení do původního integrálu:
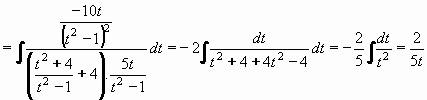
Z rovnice t2=(x+4)/(x-1) vyjádříme t:
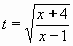
Návratem k původní proměnné x dostáváme:
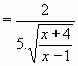 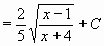
Výsledek: 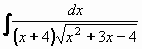 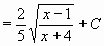
|
Eulerovy substituce racionalizují integrály s kvadratickým trojčlenem pod druhou odmocninou
vždy, ale jejich výpočet není zrovna jednoduchý. Proto se vždy nejprve snažíme najít nějaký jednodušší
postup. Ukažme si oba postupy na jednom příkladě. Nejdřív začneme (bez přemýšlení, nejsilnější zbraní) Eulerovými substitucemi.
Příklad 87:
Vypočtěte 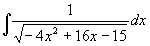
| = |
Kvadratický trojčlen lze rozložit: -4x2+16x-15 = -4(x-3/2)(x-5/2)
a můžeme tedy použít 3.Eulerovu substituci:
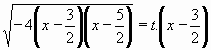
Umocněním a úpravami vyjádříme x:
-4x2+16x-15 = t2(x-3/2)2
t2=4[(5/2-x)(x-3/2)]/[(x-3/2)(x-3/2)]=4(5/2-x)/(x-3/2)
t2x-3t2/2=4(5/2-x)
x(t2+4)=3t2/2+10
x=(3t2/2+10)/(t2+4)
Difernciál x získáme derivováním:
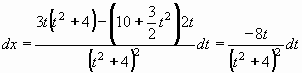
Vyjádříme také odmocninu:
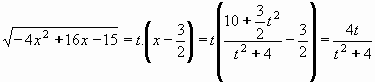
Po dosazení do původního integrálu:
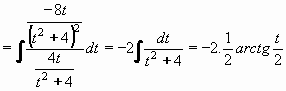
Z rovnice t2=4(5/2-x)/(x-3/2) vyjádříme t:
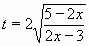
Návratem k původní proměnné x dostáváme:
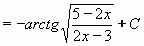
Výsledek:  
|
Nyní se zamyslíme a zjistíme, že lze příklad vyřešit elegantněji a jednoduše.
Příklad 88:
Vypočtěte 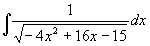
| = |
V zadání příkladu musíme "vidět" ukryté pravidlo 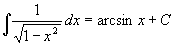 .
Nejprve upravíme výraz pod odmocnninou: .
Nejprve upravíme výraz pod odmocnninou:
-4x2+16x-15 = 1 - (4x2-16x+16) = 1 - (2x-4)2.
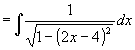
Pak již stačí použít substituci: z = 2x-4 , dz/dx=2 a tedy dx = dz/2
Tím dostáváme:
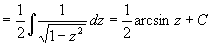
Po návratu k původní proměnné x dostáváme konečný výsledek:
= 0,5.arcsin(2x-4) + C
Výsledek: 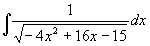 = 0,5.arcsin(2x-4) + C = 0,5.arcsin(2x-4) + C
|
Sice je výsledek v jiné formě než u předchozího postupu, ale derivováním se snadno přesvědčíme, že oba výsledky jsou správné.
Eulerovy substituce poskytují obecně i výsledek v poněkud složitější formě.
Integrál typu
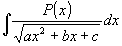
(P(x) je polynom n-tého stupně) lze vypočítat vyjmutím algebraické části integrálu (obdoba Ostrogradského metody) podle vztahu:
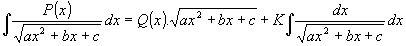 (5) (5)
Q(x) je polynom o stupeň nižší než P(x) a K konstanta. Po derivaci tohoto vztahu:
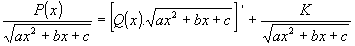
a odstranění zlomků dostaneme rovnost polynomů a metodou neurčitých součinitelů
určíme koeficienty polynomu Q(x) i konstantu K.
|
Zde je příklad:
Příklad 89:
Vypočtěte 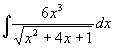
| = |
Podle vztahu (5) dostáváme (Q(x) je polynom 2.stupně):
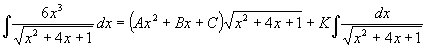
Po derivaci:
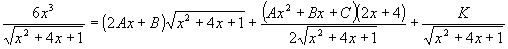
Po vynásobení odmocninou (odstranění zlomků) dostáváme rovnost polynomů:
6x3 = (2Ax+B)(x2+4x+1)+(Ax2+Bx+C)(x+2)+K
Metodou neurčitých součinitelů vypočteme koeficienty polynomu A, B, C a konstantu K:
A = 2 , B = -10 , C = 56 , K = -102
Můžeme pokračovat ve výpočtu integrálu:
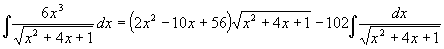
Poslední integrál:
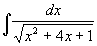
vypočteme například 1.Eulerovou substitucí a dostáváme konečný výsledek:
Výsledek: 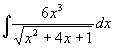 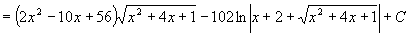
|
B. Příklady s krokovou kontrolou e-učitele
C. Příklady na procvičení učiva
Na následujících příkladech s výsledky se můžete zdokonalit ve znalostech učiva této lekce.
Pokud si nevíte s příkladem rady, užijte stručné nápovědy - Help.
| Příklady označené | A mají největší obtížnost, | B střední a | C nejmenší. |
D. Kontrolní test
E.Náhodný test
F. Hodnocení výsledků a komunikace s učitelem (tutorem)
Vytisknout certifikat
Hodnocení výsledků:
Komunikace s učitelem (tutorem):
Tato část je určena pouze pro registrované uživatele. Zaregistrujte se!
|
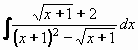
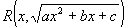 - Eulerovy substituce
- Eulerovy substituce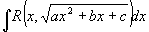 lze vždy racionalizovat (převést na integrál racionální funkce) pomocí některé ze tří Eulerových substitucí.
lze vždy racionalizovat (převést na integrál racionální funkce) pomocí některé ze tří Eulerových substitucí.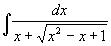
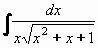
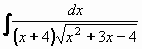
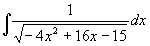
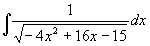
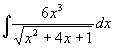
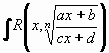 lze substitucí:
lze substitucí: 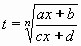 převést na integrály racionálních funkcí.
převést na integrály racionálních funkcí.
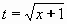 ,
,
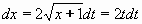
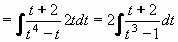
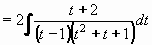
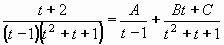
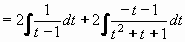
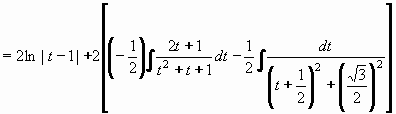
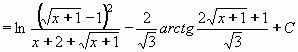
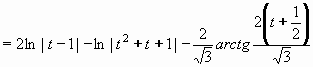
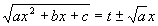
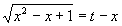
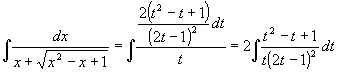
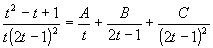
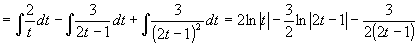
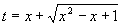
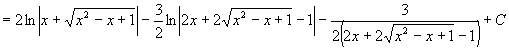
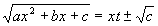
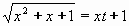
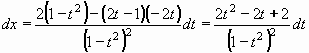
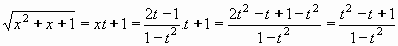
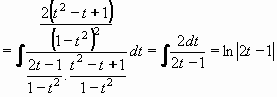
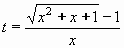
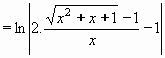
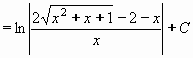
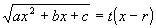
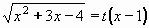
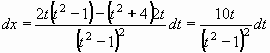
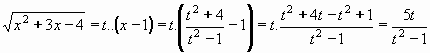
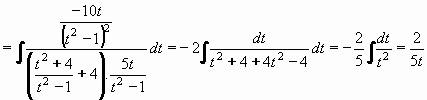
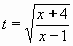
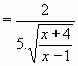
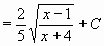
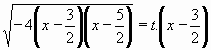
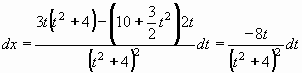
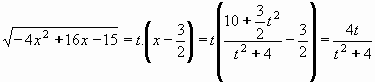
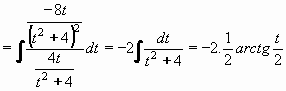
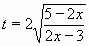
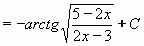
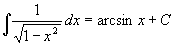 .
Nejprve upravíme výraz pod odmocnninou:
.
Nejprve upravíme výraz pod odmocnninou: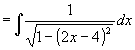
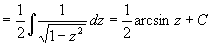
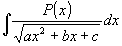
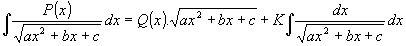 (5)
(5)