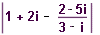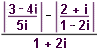Matika krokem - 3.lekce

Matika krokem - 3.lekce ...

Komplexní čísla
3.lekce - Absolutní hodnota kompl.čísla, geometrické znázornění kompl.čísel

Vytisknout

Skype výuka, doučování

A. Výklad a ukázkové příklady

Absolutní hodnota komplexního čísla

Absolutní hodnota komplexního čísla z = a + bi je reálné číslo:

(9)

Pro počítání s absolutními hodnotami komplexních čísel platí podobná pravidla jako u čísel reálných. Tedy absolutní hodnota součinu, resp. podílu komplexníxh čísel je rovna součinu, resp. podílu jejich absolutních hodnot.

Příklad 1:Určete absolutní hodnotu čísla z:

a tedy:

Komplexní číslo, jehoľ absolutní hodnota je rovna jedné, se nazývá komplexní jednotka.
Ověřte si, ľe komplexní jednotkou je např. (1 + 2i)/(2 - i)
Komplexními jednotkami jsou z čísel reálných pouze 1 a -1, z ryze imaginárních i a -i.
Komplexní čísla nelze uspořádat podle velikosti.

Geometrické znázornění komplexních čísel

Komplexní číslo můľeme chápat také jako uspořádanou dvojici reálných čísel - první je reálná část kompl.čísla a druhá imaginární část kompl.čísla. Protoľe existuje vzájemně jednoznačné přiřazení mezi mnoľinou všech uspořádaných dvojic real.čísel a mnoľinou všech bodů v rovině, je zřejmé, še můľeme komplexní čísla znázornit jako body roviny (Gaussova). Rovina komplexníxh čísel (Gaussova rovina) je rovina, jejíľ body povaľujeme za obrazy komplexníxh čísel.

Absolutní hodnota komplexního čísla je rovna vzdálenosti jeho obrazu v Gaussově rovině od počátku soustavy souřadnic.

(10)

Všechna komplexní čísla, která mají stejnou absolutní hodnotu tedy leľí na kruľnici se středem v počátku a s poloměrem |z|. Komplexní jednotky leľí na jednotkové kruľnici.

Příklad 2:V Gaussově rovině zobrazte všechna komplexní čísla z, pro něľ platí: |3 - 4i| > |z| > |-i|

Číslo z má vzdálenost od počátku menší neľ číslo 3 - 4i a větší neľ číslo -i. Protoľe |3 - 4i| = 5 a |-i| = 1 je jeho vzdálenost od počátku menší neľ 5 (vnitřek kruhu o poloměru 5) a větší neľ 1 (vnějšek kruhu s poloměrem 1). Hledaná čísla z tedy leľí v mezikruľí určeném těmito kruľnicemi (bez kruľnic).

Jsou-li dána dvě komplexní čísla x = a + bi , y = c + di potom pro absolutní hodnotu jejich rozdílu platí:
|x - y| = |(a + bi) - (c + di)| = |(a - c) + (b - d)i| =

a to je vzdálenost obrazů kompl.čísel x a y.

Absolutní hodnota rozdílu komplexních čísel určuje jejich vzdálenost v Gaussově rovině.

(11)

Příklad 3: V Gaussově rovině zobrazte všechna komplexní čísla z, pro něľ platí: |z - i|

|z + 2 - 3i|

1.způsob
|z - i| určuje vzdálenost čísla z od čísla i , |z + 2 - 3i| = |z - (-2 + 3i)| představuje vzdálenost čísla z od čísla -2 + 3i
Hledáme tedy všechna čísla z , jejichľ vzdálenost od čísla i je menší nebo rovna vzdálenosti od čísla -2 + 3i. Rovnost vzdáleností od dvou daných bodů nastává na ose úsečky učené těmito body. Poľadovaná nerovnost platí v polorovině určené touto osou (včetně osy) a bliľším bodem, tj. i.

2.způsob
Dosadíme-li za z = x + iy dostáváme:
|x + iy - i|

|x + iy + 2 - 3i|
|x + i{y - 1]|

|x + 2 + i(y - 3)|
po vyjádření absolutních hodnot a úpravách:

x² + (y - 1)²

(x + 2)² + (y - 3)²
x² + y² - 2y + 1

x² + 4x + 4 + y² - 6y + 9
0

4x - 4y +12
0

x - y + 3
Výsledek: Toto je analytické vyjádření poloroviny, která je na obrázku v 1.způsobu řešení.

Pokud výraz v absolutní hodnotě nepředstavuje rozdíl komplexních čísel, snaľíme se ho na rozdíl upravit.

Příklad 4:V Gaussově rovině zobrazte všechna komplexní čísla z, pro něľ platí:

(z nemůľe být 3) Po úpravách dostáváme:
|z| > 2|z - 3|
z

> 4(z - 3)(

)
z

> 4(z - 3)(

- 3)
z

> 4z

- 12z - 12

+ 36
3z

- 12z - 12

+ 36 < 0
z

- 4z - 4

+ 12 < 0
(z - 4)(

-4) - 4 < 0
(z - 4)(

-4) < 4
|z - 4| < 2
Výsledek: Obrazy kompl.čísel z vyplňují vnitřek kruhu (bez kruľnice a bodu [3,0]) se středem v bodě 4 a s poloměrem 2.

Příklad 5: V Gaussově rovině zobrazte všechna komplexní čísla z, pro něľ platí:

=	(z nemůľe být 0) Absolutní hodnotu upravíme: To znamená, ľe \|1 + z\| < 2 tedy \|z - (-1)\| < 2. Jedná se tedy o vnitřek kruhu se středem v bodě -1 a s poloměrem 2. Výsledek: vnitřek kruhu se středem v bodě -1 a s poloměrem 2 (bez [0,0]).

B. Příklady s krokovou kontrolou e-učitele

C. Příklady na procvičení učiva

Na následujících příkladech s výsledky se můľete zdokonalit ve znalostech učiva této lekce.
Pokud si nevíte s příkladem rady, uľijte stručné nápovědy - Help.

Příklady označené

A mají největší obtíľnost,

B střední a

C nejmenší.

1	Rozložte v součin výrazy: a) 4x²+1 b) 5 + 2y²	C	Help	Výsledek
2	Vypočtěte:	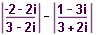B	Help	Výsledek
3	V Gaussově rovině zobrazte všechna kompl.čísla z, pro něž platí: \| z - 1 \| = 3	C	Help	Výsledek
4	Vypočtěte:	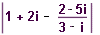B	Help	Výsledek
5	Určete všechna ryze imaginární čísla z, pro něž platí:: \|z - 1 - i\| = z	C	Help	Výsledek
6	Vypočtěte:	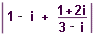B	Help	Výsledek
7	Určete všechna reálná čísla a tak, aby číslo z bylo kompl.jednotkou: z=a+i	C	Help	Výsledek
8	Vypočtěte: \|\|2 - 3i\| - i\|2 + i\|\|	B	Help	Výsledek
9	Vypočtěte:	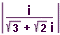B	Help	Výsledek
10	Určete všechna reálná čísla a tak, aby číslo z bylo kompl.jednotkou: z=a(3+4i)	C	Help	Výsledek
11	Vypočtěte: \|\|2 + 3i\|² + (2 + 3i)²\|	B	Help	Výsledek
12	Určete všechna reálná čísla a tak, aby číslo z bylo kompl.jednotkou: z=1/2+ai	C	Help	Výsledek
13	Vypočtěte:	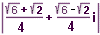B	Help	Výsledek
14	Vypočtěte:	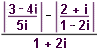A	Help	Výsledek
15	Vypočtěte:	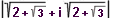B	Help	Výsledek
16	Určete všechna kompl.čísla z, která vyhovují soustavě rovnic:	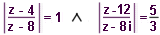A	Help	Výsledek
17	Určete všechna ryze imaginární čísla z, pro něž platí:: \|z + 1\| = \|z - 2i\|	B	Help	Výsledek
18	Zjednodušte: i.\|z + i\|² - (1 + i) + \|z + i\|² - (i + 1).\|z\|², kde z je kompl.číslo	B	Help	Výsledek
19	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| z - i \| = 2	C	Help	Výsledek
20	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \|- 4 - 2i\|.\| z - 4 - 2i \| = 0	B	Help	Výsledek
21	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \|+ 12 \| = 12	C	Help	Výsledek
22	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| z -4 + 4i \|.\| 1 - z \|.\| (z - )/2\| = 0	B	Help	Výsledek
23	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| z. - 2 \|.\| z. - 4 \|.\| \|z\| - 4 \| = 0	B	Help	Výsledek
24	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| z - 3i \| 10	C	Help	Výsledek
25	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: 1 \| z - 2i \| 4	B	Help	Výsledek
26	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| z - i \| < 6	C	Help	Výsledek
27	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: 0,4 \| z + 1 - i \| 2,4	B	Help	Výsledek
28	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| z + 1 - 4i \| > 8	C	Help	Výsledek
29	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| z - 1 \| \| z + 1 \|	B	Help	Výsledek
30	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí:	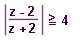A	Help	Výsledek
31	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| z - i \| \| z + i \|	B	Help	Výsledek
32	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| z + - i \| < 1	B	Help	Výsledek
33	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí:	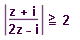A	Help	Výsledek
34	Zapište rovnici, která má obraz oboru pravdivosti v Gaus.rovině osu ůsečky určené obrazy čísel 2, i.	B	Help	Výsledek
35	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| z + 1 - i \| 0,5	C	Help	Výsledek
36	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| z - 1 \| \| z + 2i \| a současně \| z - 2 \| < 4	B	Help	Výsledek
37	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí:	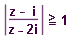A	Help	Výsledek
38	V Gaus.r. zobrazte k.čísla z, pro něž platí: 2 < \| z - 1 + 2i \| < 7 \| z + 2i \| a současně \| z + 1 + 3i \| 2	B	Help	Výsledek
39	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| 1 - i \| > \|z\| 1	C	Help	Výsledek
40	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí:	B	Help	Výsledek
41	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| 2 - 3i \| \|z\| > \| 1 + 2i \|	C	Help	Výsledek
42	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí:	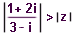B	Help	Výsledek
43	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| z + i \| \| z + 1 \|	C	Help	Výsledek
44	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí:	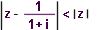B	Help	Výsledek
45	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí:	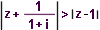B	Help	Výsledek
46	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí:	B	Help	Výsledek
47	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí zároveň: \|z\| 1 , \|z - i\| \|z\| , \|z-1\| 1	A	Help	Výsledek
48	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí:	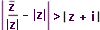B	Help	Výsledek
49	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí zároveň: \|z\| 2 , \|z +1-i\| , \|z-1-i\|	B	Help	Výsledek
50	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí zároveň: \|z-1-i\|=1 , \|z-i\|=\|z-1\|	B	Help	Výsledek
51	V množině C řešte rovnici s neznámou z: \|z\| - z = 1 + 2i	B	Help	Výsledek
52	V množině C řešte rovnici s neznámou z: z² + \|z\| = 0	A	Help	Výsledek
53	V množině C řešte rovnici s neznámou z:	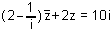B	Help	Výsledek
54	V množině C řešte rovnici s neznámou z:	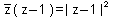B	Help	Výsledek
55	Rozložte v součin výrazy: a) 4x²+1 b) 5 + 2y²	C	Help	Výsledek
56	Vypočtěte:	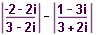B	Help	Výsledek
57	V Gaussově rovině zobrazte všechna kompl.čísla z, pro něž platí: \| z - 1 \| = 3	C	Help	Výsledek
58	Vypočtěte:	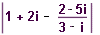B	Help	Výsledek
59	Určete všechna ryze imaginární čísla z, pro něž platí:: \|z - 1 - i\| = z	C	Help	Výsledek
60	Vypočtěte:	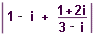B	Help	Výsledek
61	Určete všechna reálná čísla a tak, aby číslo z bylo kompl.jednotkou: z=a+i	C	Help	Výsledek
62	Vypočtěte: \|\|2 - 3i\| - i\|2 + i\|\|	B	Help	Výsledek
63	Vypočtěte:	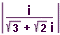B	Help	Výsledek
64	Určete všechna reálná čísla a tak, aby číslo z bylo kompl.jednotkou: z=a(3+4i)	C	Help	Výsledek
65	Vypočtěte: \|\|2 + 3i\|² + (2 + 3i)²\|	B	Help	Výsledek
66	Určete všechna reálná čísla a tak, aby číslo z bylo kompl.jednotkou: z=1/2+ai	C	Help	Výsledek
67	Vypočtěte:	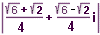B	Help	Výsledek
68	Vypočtěte:	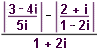A	Help	Výsledek
69	Vypočtěte:	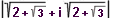B	Help	Výsledek
70	Určete všechna kompl.čísla z, která vyhovují soustavě rovnic:	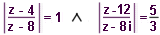A	Help	Výsledek
71	Určete všechna ryze imaginární čísla z, pro něž platí:: \|z + 1\| = \|z - 2i\|	B	Help	Výsledek
72	Zjednodušte: i.\|z + i\|² - (1 + i) + \|z + i\|² - (i + 1).\|z\|², kde z je kompl.číslo	B	Help	Výsledek
73	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| z - i \| = 2	C	Help	Výsledek
74	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \|- 4 - 2i\|.\| z - 4 - 2i \| = 0	B	Help	Výsledek
75	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \|+ 12 \| = 12	C	Help	Výsledek
76	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| z -4 + 4i \|.\| 1 - z \|.\| (z - )/2\| = 0	B	Help	Výsledek
77	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| z. - 2 \|.\| z. - 4 \|.\| \|z\| - 4 \| = 0	B	Help	Výsledek
78	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| z - 3i \| 10	C	Help	Výsledek
79	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: 1 \| z - 2i \| 4	B	Help	Výsledek
80	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| z - i \| < 6	C	Help	Výsledek
81	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: 0,4 \| z + 1 - i \| 2,4	B	Help	Výsledek
82	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| z + 1 - 4i \| > 8	C	Help	Výsledek
83	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| z - 1 \| \| z + 1 \|	B	Help	Výsledek
84	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí:	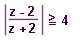A	Help	Výsledek
85	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| z - i \| \| z + i \|	B	Help	Výsledek
86	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| z + - i \| < 1	B	Help	Výsledek
87	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí:	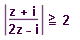A	Help	Výsledek
88	Zapište rovnici, která má obraz oboru pravdivosti v Gaus.rovině osu ůsečky určené obrazy čísel 2, i.	B	Help	Výsledek
89	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| z + 1 - i \| 0,5	C	Help	Výsledek
90	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| z - 1 \| \| z + 2i \| a současně \| z - 2 \| < 4	B	Help	Výsledek
91	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí:	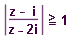A	Help	Výsledek
92	V Gaus.r. zobrazte k.čísla z, pro něž platí: 2 < \| z - 1 + 2i \| < 7 \| z + 2i \| a současně \| z + 1 + 3i \| 2	B	Help	Výsledek
93	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| 1 - i \| > \|z\| 1	C	Help	Výsledek
94	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí:	B	Help	Výsledek
95	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| 2 - 3i \| \|z\| > \| 1 + 2i \|	C	Help	Výsledek
96	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí:	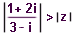B	Help	Výsledek
97	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí: \| z + i \| \| z + 1 \|	C	Help	Výsledek
98	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí:	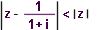B	Help	Výsledek
99	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí:	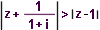B	Help	Výsledek
100	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí:	B	Help	Výsledek
101	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí zároveň: \|z\| 1 , \|z - i\| \|z\| , \|z-1\| 1	A	Help	Výsledek
102	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí:	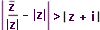B	Help	Výsledek
103	V Gaus.rovině zobrazte všechna kompl.čísla z, pro něž platí zároveň: \|z-1-i\|=1 , \|z-i\|=\|z-1\|	B	Help	Výsledek
104	V množině C řešte rovnici s neznámou z: \|z\| - z = 1 + 2i	B	Help	Výsledek
105	V množině C řešte rovnici s neznámou z: z² + \|z\| = 0	A	Help	Výsledek
106	V množině C řešte rovnici s neznámou z:	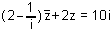B	Help	Výsledek
107	V množině C řešte rovnici s neznámou z:	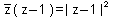B	Help	Výsledek