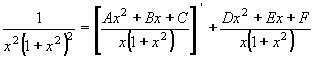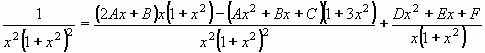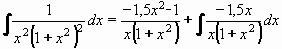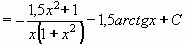A. Výklad a ukázkové příklady
Integrování racionálních funkcí
Integrování racionální funkce provádíme tak, že racionální funkci rozložíme na součet mnohočlenu a jednoduchých racionálních funkcí, které
dovedeme integrovat - říkáme jim parciální zlomky.
Tento postup demonstruje příklad 70:
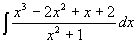 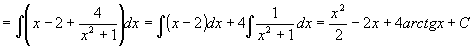
Integrování racionálních funkcí probereme ve dvou krocích:
A) Nejdřív si ukážeme, které zlomky řadíme mezi parciální a jak se integrují.
B) Ostatní racionální funkce budeme rozkládat na mnohočlen a parciální zlomky a ty známým způsobem integrovat.
A) Integrování parciálních zlomků
Parciální zlomky rozdělujeme do čtyř typů:
| I. |
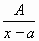 |
II. |
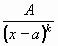 |
III. |
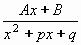 | (x2+px+q bez
reálných kořenů) |
IV. |
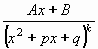 | (x2+px+q bez
reálných kořenů) |
Na integrování zlomku typu I. 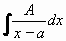 použijeme substitucí t = x-a , dx = dt a pravidla
použijeme substitucí t = x-a , dx = dt a pravidla 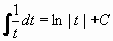
Na integrování zlomku typu II. 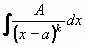 použijeme také substituci
t = x-a , dx = dt a pravidla použijeme také substituci
t = x-a , dx = dt a pravidla 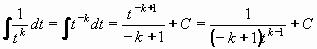
Příklad 75:
Vypočtěte 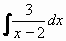
| = |
Položíme t = x - 2 , potom dx = dt a dostáváme:
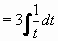 = 3.ln|t| + C = 3.ln|t| + C
a po návratu k původní proměnné x dostáváme konečný výsledek:
= 3.ln|x-2| + C
Výsledek: 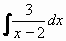 = 3.ln|x-2| + C = 3.ln|x-2| + C
|
Příklad 76:
Vypočtěte 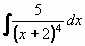
| = |
Položíme t = x + 2 , potom dx = dt a dostáváme:
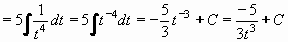
a po návratu k původní proměnné x dostáváme konečný výsledek:
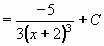
Výsledek: 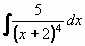 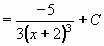
|
Další dva typy jsou podstatně obtížnější.
Zlomek typu III. 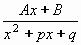 rozložíme nejprve na součet dvou zlomků. rozložíme nejprve na součet dvou zlomků.
První bude mít v čitateli derivaci jmenovatele a povede po substituci t = x2+px+q na ln|x2+px+q| + C
Druhý bude mít v čitateli konstantu a ve jmenovateli x2+px+q. Úpravami ho převedeme na typ 1/(t2+a2) a povede
po substituci na arctgt + C.
Příklad 77:
Vypočtěte 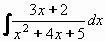
| = |
Kvadratický trojčlen x2+5x+4 nelze rozložit (D = 16-4.5 = -4), jde tedy o typ III.
Nejprve integrovanou funkci (zlomek) rozložíme na dva zlomky.
První bude mít v čitateli derivaci jmenovatele a po integraci povede na přirozený logaritmus.
Druhý bude mít v čitateli pouze konstantu a po integraci vznikne arkus tangens.
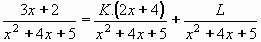
Čitatel prvního zlomku na pravé straně musí "vyrovnat" počet x na levé straně a snadno zjistíme, že K=3/2=1,5.
Druhý zlomek musí "dorovnat" zbytek - první zlomek dává 1,5(2x+4)=3x+6 , musíme tedy odečíst 4, proto L= - 4.
Původní integrál můžeme napsat jako součet integrálů:
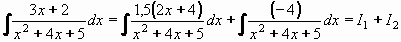
Integrál I1 převedem pomocí substituce t = x2+4x+5 , dt/dx = 2x+4 , tedy dx = dt/(2x+4) na integrál
elementární funkce, vedoucí na přirozený logaritmus:
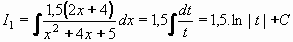 = 1,5.ln|x2+4x+5| + C = 1,5.ln|x2+4x+5| + C
Výpočet integrálu I2 bude horší. Nejprve jmenovatele převedeme na tvar (x + r)2+s2:
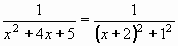
Substitucí t = x+2 , dx = dt převedeme na integrál elementární funkce, vedoucí na arkus tangens:
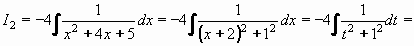 - 4arctgt + C = -4arctg(x+2) + C - 4arctgt + C = -4arctg(x+2) + C
Výsledek: 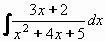 = 1,5.ln|x2+4x+5| - 4arctg(x+2) + C = 1,5.ln|x2+4x+5| - 4arctg(x+2) + C
|
Zlomek typu IV. 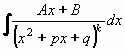 nejprve rozložíme na dva integrály stejným způsobem jako u typu III. nejprve rozložíme na dva integrály stejným způsobem jako u typu III.
První bude mít v čitateli derivaci kvadratického trojčlenu jmenovatele a druhý pouze konstantu.
První integrál substitucí převedeme na integrál typu:
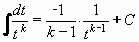
Druhý integrál upravíme takto:
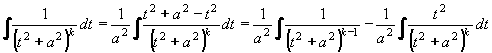 (*) (*)
Postupně tedy snižujeme stupeň jmenovatele (první integrál) a zbývající část (druhý integrál) počítáme metodou per partes.
Příklad 78:
Vypočtěte 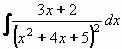
| = |
Kvadratický trojčlen x2+5x+4 nelze rozložit (D = 16-4.5 = -4), jde tedy o typ III.
Nejprve integrovanou funkci (zlomek) rozložíme na dva zlomky.
První bude mít v čitateli derivaci kvadratického trojčlenu jmenovatele a druhý bude mít v čitateli pouze konstantu.
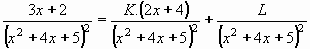
Čitatel prvního zlomku na pravé straně musí "vyrovnat" počet x na levé straně a snadno zjistíme, že K=3/2=1,5.
Druhý zlomek musí "dorovnat" zbytek - první zlomek dává 1,5(2x+4)=3x+6 , musíme tedy odečíst 4, proto L= - 4.
Původní integrál můžeme napsat jako součet integrálů:
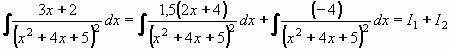
Integrál I1 převedem pomocí substituce t = x2+4x+5 , dt/dx = 2x+4 , tedy dx = dt/(2x+4) na integrál
elementární funkce xn:
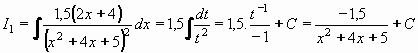
Výpočet integrálu I2 bude opět horší. Nejprve upravíme jmenovatele (jako v předchozím příkladě) a použijeme substituci t = x + 2:
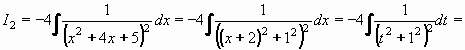
Potom použijeme uvedené úpravy (*) , abychom mohli použít pravidel pro elementární funkce:
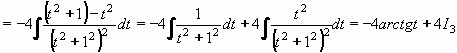
Integrál I3vypočteme metodou per partes. Zvolíme u = t , v' = t/(t2+1)2.
Potom u' = 1 a 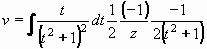
Položili jsme z = t2 + 1 , dx = dz/2t.
Tím můžeme dokončit výpočet I3:
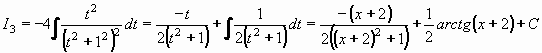
Pro výsledný integrál potom platí:
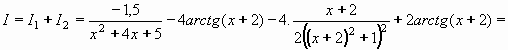
Po úpravách dostáváme konečný výsledek:
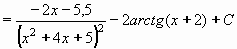
Výsledek: 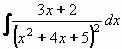 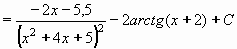
|
Tyto příklady potvrzují obecný závěr:
|
Integrál libovolné racionální funkce lze vyjádřit pomocí racionální funkce, logaritmu a arkustangens.
|
B) Rozklad racionální lomené funkce v parciální zlomky.
Pokud je v racionální lomené funkci 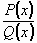 stupeň mnohočlenu v čitateli vyšší ne ž stupeň mnohočlenu ve jmenovateli, upravíme ji
nejprve dělením na součet mnohočlenu a racionální ryze lomené funkce (stupeň mnohočlenu v čitateli je menší než stupeň mnohočlenu ve jmenovateli). stupeň mnohočlenu v čitateli vyšší ne ž stupeň mnohočlenu ve jmenovateli, upravíme ji
nejprve dělením na součet mnohočlenu a racionální ryze lomené funkce (stupeň mnohočlenu v čitateli je menší než stupeň mnohočlenu ve jmenovateli).
¨
Potom mnohočlen ve jmenovateli Q(x) rozložíme na součin kořenových činitelů a kvadratických výrazů, které nejsou rozložitelné:
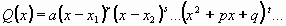
kde x1 je kořen o násobnosti r, x2 je kořen o násobnosti s.
Ryze lomenou funkci 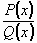 lze pak jednoznačně rozložit v součet parciálních zlomků takto: lze pak jednoznačně rozložit v součet parciálních zlomků takto:
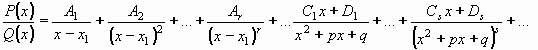 (1) (1)
|
Pozor! Kořen s násobností k přispívá do rozkladu k členy (zlomky)1
Neznámá čísla A1, A2, ...,B1, B2, ... ,C1,C2, ... lze určit:
B1) metodou neurčitých součunitelů
B2) Ostrogradského metodou
Integrál racionální funkce 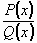 pak vypočteme jako součet integrálů získaných parciálních zlomků
postupem vysvětleným v části A. pak vypočteme jako součet integrálů získaných parciálních zlomků
postupem vysvětleným v části A.
B1) Metoda neurčitých součinitelů
V rovnici :
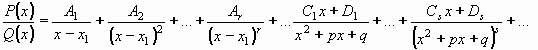
odstraníme zlomky (vynásobením Q(x)) a dostaneme rovnost mnohočlenů. Porovnáním koeficientů u stejných mocnin
proměnné x dostaneme soustavu rovnic, ze kterých neznámé konstanty A1, A2, ...,B1, B2, ... ,C1,C2, ...
vypočteme.
Nejprve se na příkladech ukážeme výpočet integrálů racionální ryze lomené funkce.
Příklad 79:
Vypočtěte 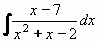
| = |
Jmenovatele rozložíme: x2 + x - 2 = (x + 2).(x - 1)
Rozklad na součet parciálních zlomků bude vypadat:
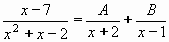
Odstraníme zlomky:
x - 7 = A(x - 1) + B(x + 2)
Odstraníme závorky:
x - 7 = Ax - A -Bx + 2B
Porovnáníím koeficientů u odpovídajích si členů (stejných mocnn x) dostáváme soustavu rovnc:
1 = A + B , -7 = -A + 2B
Součtovou metodou snadno zjistíme, že B =-2 a potom A = 3
Rozklad na parciální zlomky je:
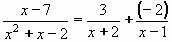
Nyní převedeme daný integrál na součet iintegrálů parciálních zlomků:
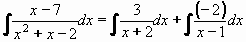
Integrály parciálních zlomků snadno vypočteme podle postupu v části A:
= 3ln|x + 2| - 2ln|x - 1| + C.
Výsledek: 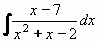 = 3ln|x + 2| - 2ln|x - 1| + C = 3ln|x + 2| - 2ln|x - 1| + C
|
Jak se postupuje u násobných kořenů ukazuje další příklad.
Příklad 80:
Vypočtěte 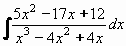
| = |
Rozklad jmenovatele vypadá: x3 - 4x2 + 4x = x.(x - 2)2
Rozklad na součet parciálních zlomků bude vypadat:
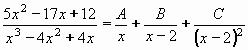
Odstraníme zlomky:
5x2 - 17x + 12 = A(x - 2)2 + Bx(x - 2) + Cx
Odstraníme závorky:
5x2 - 17x + 12 = Ax2 - 4Ax + 4A + Bx2 - 2Bx + Cx
Porovnáníím koeficientů u odpovídajích si členů (stejných mocnn x) dostáváme soustavu rovnc:
5 = A + B , -17 = -4A - 2B + C , 12 = 4A
Snadno získáváme postupně A = 3 , B = 2 , C = -1
Daný integrál napíšeme jako součet iintegrálů parciálních zlomků:
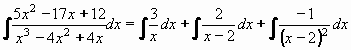
Po výpočtu integrálů parciálních zlomků dostáváme::
= 3ln|x| + 2ln|x - 2| + 1/(x - 2) + C
Výsledek: 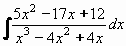 = 3ln|x| + 2ln|x - 2| + 1/(x - 2) + C = 3ln|x| + 2ln|x - 2| + 1/(x - 2) + C
|
Jestliže se nejedná o racionální ryze lomenou funkci, převedeme ji dělením na součet mnohočlenu a racionální ryze lomené funkce.
Příklad 81:
Vypočtěte 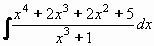
| = |
Nejprve vydělíme čitatele jmenovatelem.
(x4 + 2x3 + 2x2 + 5) : (x3 + 1) = x + 2
-x4 -x2
23 +2x2-x+5
-23 -2
2x2-x+3
Tím vznikne součet mnohočlenu a racionální ryze lomené funkce.:
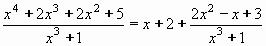
Teď rozložíme racionální ryze lomenou funkci na parciální zlomky.
Rozklad jmenovatele vypadá:
x3 + 1 = (x + 1)(x2 - x + 1)
Rozklad na parciální zlomky má tvar:
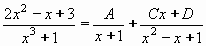
Odstraníme zlomky:
2x2 - x + 3 = A(x2 - x + 1) + (Cx + D)(x + 1)
Odstraníme závorky:
2x2 - x + 3 = Ax2 - Ax + A + Cx2 + Cx + Dx + D
Porovnáníím koeficientů u odpovídajích si členů (stejných mocnn x) dostáváme soustavu rovnc:
2 = A + C , -1 = -A + C + D , 3 = A + D
Řešením soustavy získáme A = 2 , C = 0 , D = 1 a rozklad na parciální zlomky je:
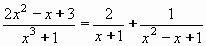
Rozklad původní funkce lze zapsat takto:
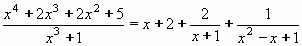
A integrál původní funkce lze vyjádřit:
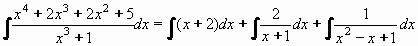
Po výpočtu prvních tří členů:dostáváme:
= x2/2 + 2x + 2ln|x + 1| + I1
Poslední integrál je integrálem parciálního zlomku typu III z části A:
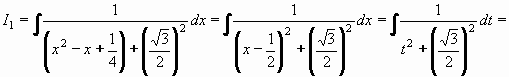
(po substituci t = x - 1/2 , dx = dt)
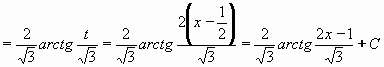
Tím můžeme dosadit za I1 a dostáváme konečný výsledek:
Výsledek: 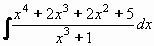 
|
B2) Dosazovací metoda
Někdy bývá řešení soustavy rovnic při určování neznámých součinitelů značně náročné. Potom lze s výhodou použít
metodu dosazovací, kterou lze použít pro jednoduché kořeny.
Do rovnice vyjadřující rovnost polynomů (po odstranění zlomků) dosadíme za proměnnou x kořen a vypočteme příslušný součinitel.
Rozklad na parciální zlomky z příkladu 79 provedem dosazovací metodou:
Příklad 82:
Vypočtěte 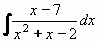
| = |
První kroky uděláme stejně jako v příkladu 79.
Jmenovatele rozložíme: x2 + x - 2 = (x + 2).(x - 1)
Rozklad na součet parciálních zlomků bude vypadat:
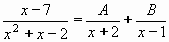
Odstraníme zlomky:
x - 7 = A(x - 1) + B(x + 2)
Nyní nebudeme řešit soustavu rovnic, ale dosazením kořene x = 1 získáme :
-6 = 3.B
a tedy B = -2
Dosazením x = -2 vypočteme koeficient A:
-9 = -3.A
A = 3
Další postup už bude zase stejný jako v př. 79.
Rozklad na parciální zlomky je:
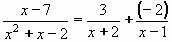
Nyní převedeme daný integrál na součet iintegrálů parciálních zlomků:
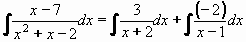
Integrály parciálních zlomků snadno vypočteme podle postupu v části A:
= 3ln|x + 2| - 2ln|x - 1| + C.
Výsledek: 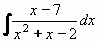 = 3ln|x + 2| - 2ln|x - 1| + C = 3ln|x + 2| - 2ln|x - 1| + C
|
Obě metody lze kombinovat. Dosazovací metodou vypočteme některé z hledaných součinitelů a zbývající dopočteme pomocí
metody neurčitých koeficientů.
Příklad 80 lze kombinací těchto metod vypočítat následovně:
Příklad 83:
Vypočtěte 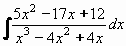
| = |
Podle příkladu 80 dostáváme:
Rozklad na součet parciálních zlomků bude vypadat:
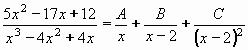
Odstraníme zlomky:
5x2 - 17x + 12 = A(x - 2)2 + Bx(x - 2) + Cx
Odstraníme závorky:
5x2 - 17x + 12 = Ax2 - 4Ax + 4A + Bx2 - 2Bx + Cx
Nyní dosadíme x = 0 a vypočteme A:
12 = 4.A a tedy A = 3
Dosazením x = 2 získáme C:
-2 = 2.C a tedy C = -1
Porovnáníím koeficientů u odpovídajích si členů (stejných mocnn x) dostáváme soustavu rovnc:
5 = A + B , -17 = -4A - 2B + C , 12 = 4A
Z rovnice -17 = -4A - 2B + C dostáváme C = -1
Dál postupujeme stejně:
Daný integrál napíšeme jako součet iintegrálů parciálních zlomků:
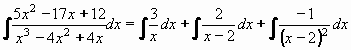
Po výpočtu integrálů parciálních zlomků dostáváme::
= 3ln|x| + 2ln|x - 2| + 1/(x - 2) + C
Výsledek: 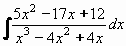 = 3ln|x| + 2ln|x - 2| + 1/(x - 2) + C = 3ln|x| + 2ln|x - 2| + 1/(x - 2) + C
|
B3) Ostrogradského metoda (vyjmutí racionální části integrálu)
Integrál racionální funkce má obecně tři části. Racionální část a časti vyjadřené pomocí přirozeného logaritmu a arkustangens.
Ostrogradského metoda umožňuje vyjádřit racionální část výsledku, je-li integrovanou funkcí racionální ryze lomená funce tavru
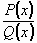 , kde Q(x) = (x-x1)k...(x2+px+q)l... a aspoň jeden z exponentů k,..,l.. je větší než 1. , kde Q(x) = (x-x1)k...(x2+px+q)l... a aspoň jeden z exponentů k,..,l.. je větší než 1.
Racionální část 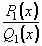 lze potom vyjádřit užitím vztahu: lze potom vyjádřit užitím vztahu:
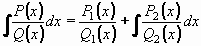 (2) (2)
|
kde Q1(x) má exponenty závorek o jednotku menší:
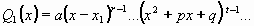
a pro Q2(x) platí: Q(x) = Q1(x).Q2(x) , tedy:
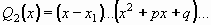
Pro určení čitatelů P1(x) a P2(x) použijeme metodu neurčitých koeficientů a
Ostrogradského vztahu:
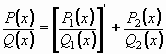 (3) (3)
|
který je ekvivalentní vztahu (2).
Konec teorie a je tu příklad.
Příklad 84:
Vypočtěte 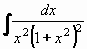
| = |
Jmenovatel Q1(x) racionální části má exponenty o jednotku menší: Q1(x) = x.(1 + x2)
Druhý jmenovatel Q2(x) = x.(1 + x2) ,
aby součin Q1(x).Q2(x) = x.2(1 + x2)2
Pro čitatele P1(x) a P2(x) musí platit podle (3) :
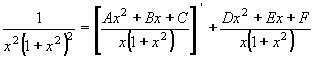
Po výpočtu derivace vznikne:
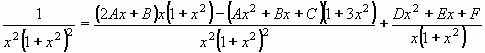
Odstraněním zlomků dostáváme rovnost polynomů:
1 = (2Ax2+Bx)(1+x2)-(Ax2+Bx+C)(1+3x2)+(Dx3+Ex2+Fx)(1+x2)
Úpravou získáváme rovnici:
1 = Dx5+(E-A).x4+(D-2B+F).x3+(A-3C+E).x2+Fx-C
Na základě rovnosti koeficientů členů polynomů stejných stupňů postupně dostáváme:
C = -1 , F = 0 , D = 0 , B = 0 , E = -3/2 , A = -3/2
Nyní můžeme použít vztah (1) a vypočítat původní integrál:
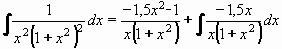
Po vykrácení x (v druhém integrálu) dostáváme konečný výsledek:
Výsledek: 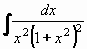 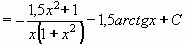
|
B. Příklady s krokovou kontrolou e-učitele
C. Příklady na procvičení učiva
Na následujících příkladech s výsledky se můžete zdokonalit ve znalostech učiva této lekce.
Pokud si nevíte s příkladem rady, užijte stručné nápovědy - Help.
| Příklady označené | A mají největší obtížnost, | B střední a | C nejmenší. |
D. Kontrolní test
E.Náhodný test
F. Hodnocení výsledků a komunikace s učitelem (tutorem)
Vytisknout certifikat
Hodnocení výsledků:
Komunikace s učitelem (tutorem):
Tato část je určena pouze pro registrované uživatele. Zaregistrujte se!
|
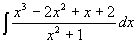
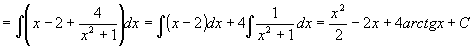
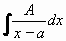 použijeme substitucí t = x-a , dx = dt a pravidla
použijeme substitucí t = x-a , dx = dt a pravidla 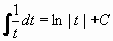
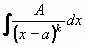 použijeme také substituci
t = x-a , dx = dt a pravidla
použijeme také substituci
t = x-a , dx = dt a pravidla 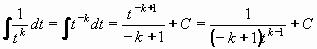
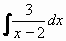
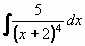
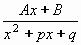 rozložíme nejprve na součet dvou zlomků.
rozložíme nejprve na součet dvou zlomků.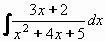
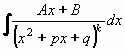 nejprve rozložíme na dva integrály stejným způsobem jako u typu III.
nejprve rozložíme na dva integrály stejným způsobem jako u typu III.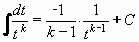
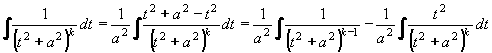 (*)
(*)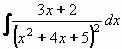
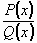 stupeň mnohočlenu v čitateli vyšší ne ž stupeň mnohočlenu ve jmenovateli, upravíme ji
nejprve dělením na součet mnohočlenu a racionální ryze lomené funkce (stupeň mnohočlenu v čitateli je menší než stupeň mnohočlenu ve jmenovateli).
stupeň mnohočlenu v čitateli vyšší ne ž stupeň mnohočlenu ve jmenovateli, upravíme ji
nejprve dělením na součet mnohočlenu a racionální ryze lomené funkce (stupeň mnohočlenu v čitateli je menší než stupeň mnohočlenu ve jmenovateli).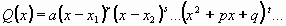
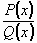 lze pak jednoznačně rozložit v součet parciálních zlomků takto:
lze pak jednoznačně rozložit v součet parciálních zlomků takto: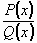 pak vypočteme jako součet integrálů získaných parciálních zlomků
postupem vysvětleným v části A.
pak vypočteme jako součet integrálů získaných parciálních zlomků
postupem vysvětleným v části A.
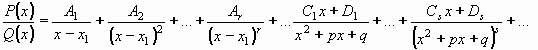
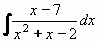
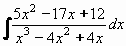
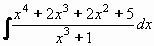
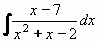
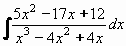
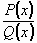 , kde Q(x) = (x-x1)k...(x2+px+q)l... a aspoň jeden z exponentů k,..,l.. je větší než 1.
, kde Q(x) = (x-x1)k...(x2+px+q)l... a aspoň jeden z exponentů k,..,l.. je větší než 1. 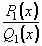 lze potom vyjádřit užitím vztahu:
lze potom vyjádřit užitím vztahu: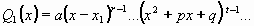
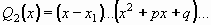
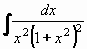
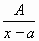
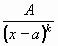
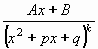
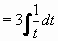 = 3.ln|t| + C
= 3.ln|t| + C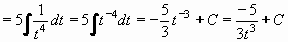
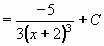
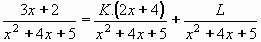
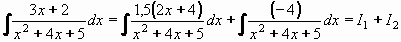
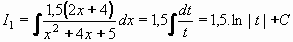 = 1,5.ln|x2+4x+5| + C
= 1,5.ln|x2+4x+5| + C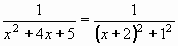
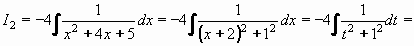 - 4arctgt + C = -4arctg(x+2) + C
- 4arctgt + C = -4arctg(x+2) + C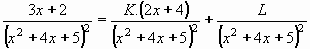
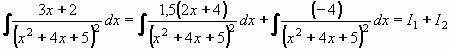
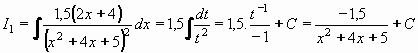
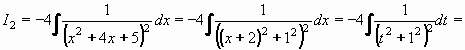
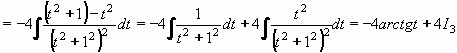
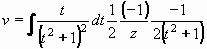
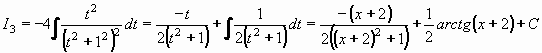
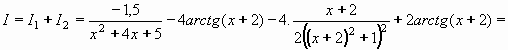
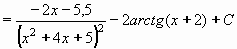
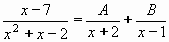
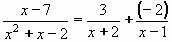
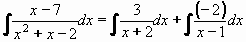
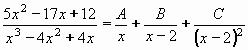
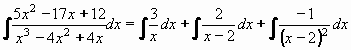
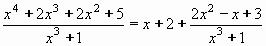
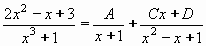
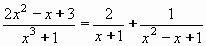
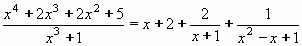
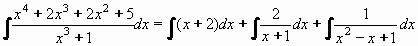
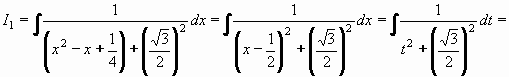
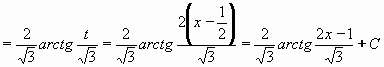
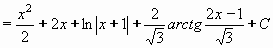
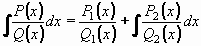 (2)
(2)
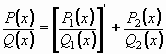 (3)
(3)