A. Výklad a ukázkové příklady
Určitý integrál
Ke každé funkci spojité v intervalu <a,b> existuje primitivní funkce v tomto intervalu.
Pomocí primitivní funkce je definován tzv. určitý integrál a umožňuje řešit řadu úloh např. na výpočet
obsahu rovinných útvarů a objemu rotačních těles.
Nechtˇ F je primitivní funkcí k funkci f v intervalu I. Potom rozdíl F(b) - F(a) funkčních hodnot funkce F v libovolných
bodech a,b tohoto intervalu se nazývá Newtonův určitý integrál funkce f v mezích od a do b a značí se:
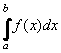
číslo a se nazývá dolní mez, číslo b horní mez integrálu, funkce f integrand, dx diferenciál x označující
integrační proměnnou. Platí tedy:
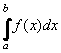 = F(b) - F(a) = F(b) - F(a)
| (49) |
|
Určitý integrál je na rozdíl od neurčitého integrálu jednoznačně definované reálné číslo.
Jakou má toto číslo geometrickou interpretaci?
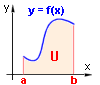
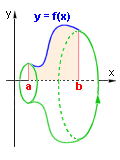
Mějme dánu spojitou a nezápornou funkci f v intervalu <a,b>.Potom udává učitý integrál 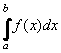 obsah útvaru U (na obrázku) ohraničeného grafem funkce f, osou x a přímkami x = a , x = b.
obsah útvaru U (na obrázku) ohraničeného grafem funkce f, osou x a přímkami x = a , x = b.
Tedy: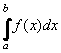 = S(U) = S(U)
Příklad 61:
Vypočtěte 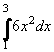
| = |
Nejprve podle definice zjistíme primitivní funkci k funkci f(x) = 6x2.
Tedy F(x) = 2x3 a potom vypočteme rozdíl F(3) - F(1) = 2.33 - 2.13.
Pro zápis řešení užíváme výhodnějšího způsobu, kdy primitivní funkci zapíšeme do hratanaté závorky a meze připíšeme.
Potom dosadíme horní mez a dolní mez a odečteme (v tomto pořadí):
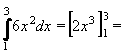 2.33 - 2.13 = 52 2.33 - 2.13 = 52
Výsledek: 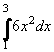 = 52 = 52
|
Výpočet určitého integrálu
Při výpočtu primitivní funkce používáme pravidel a vět poznaných v předchozí lekci. Navíc uvedeme některé
poučky o mezích integrálu:
Při záměně mezí určitého integrálu se mění znaménko, tedy: 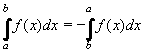
Je-li funkce f spojitá v intervalu <a,b> a bod c je jeho vnitřním bodem, pak lze integrál vyjádřit jako součet
integrálů v dílčích intervalech: 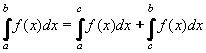
| (50) |
|
Příklad 62:
Vypočtěte 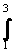 x(1 - x)2dx x(1 - x)2dx
| = |
Nejprve podle definice zjistíme primitivní funkci. Závorku umocníme a roznásobíme:
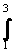 x(1 - x)2dx = x(1 - x)2dx = 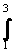 x(1 - 2x + x2)dx = x(1 - 2x + x2)dx =
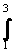 (x - 2x2 + x3)dx = (x - 2x2 + x3)dx =
Nyní integrujeme člen po členu:
= [x2/2 - 2x3/3 + x4/4]13 =
Nakonec dosadíme meze a odečteme:
= (9/2 - 2.27/3 + 81/4) - (1/2 - 2/3 + 1/4) = 99/4 - 18 - 3/4 + 2/3 = 6 + 2/3 = 20/3
Výsledek: 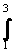 x(1 - x)2dx = 20/3 x(1 - x)2dx = 20/3
|
Lze samozřejmě používat i metodu per partes a substituční metodu. U substituční metody je třeba pamatovat na to, že
při zavedení pomocné proměnné se také změní integrační meze!
Příklad 63:
Vypočtěte 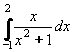
| = |
Použijeme substituci t = x2 + 1
Potom t' = 2x = dt/dx .
Vyjádříme dx: dx = dt/2x
Nyní nesmíme zapomenout přepočítat meze integrálu. Vypočteme odpovídající hodnoty proměnné t pro pro původní meze x.
t(-1) = x2 + 1 = (-1)2 + 1 = 2
t(2) = x2 + 1 = 22 + 1 = 5
Nyní již můžeme dosadit:
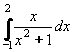 = = 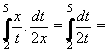
Tento integrál snadno vypočteme a dosadíme meze:
= [0,5.lnt]25 = 0,5.ln5 - 0,5.ln2 = 0,5.ln2,5
Výsledek: 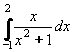 = 0,5.ln2,5 = 0,5.ln2,5
|
Příklad 64:
Vypočtěte 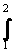 (3x + 2)lnx dx (3x + 2)lnx dx
| = |
Použijeme metodu per partes.
Zvolíme za u´= 3x + 2 a za v = lnx
Potom bude u = 3x2/2 + 2x a v' = 1/x
Po dosazení dostáváme:
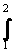 (3x + 2)lnx dx =
[(3x2/2 + 2x)lnx]12 - (3x + 2)lnx dx =
[(3x2/2 + 2x)lnx]12 - 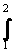 (3x2/2 + 2x)/x dx =
= (6 + 4)ln2 - (3/2 + 2)ln1 - (3x2/2 + 2x)/x dx =
= (6 + 4)ln2 - (3/2 + 2)ln1 - 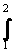 (3x/2 + 2)dx =
10ln2 - [3x2/4 + 2x]12 = 10ln2 - 7 + 2,75 = 10ln2 - 4,25 (3x/2 + 2)dx =
10ln2 - [3x2/4 + 2x]12 = 10ln2 - 7 + 2,75 = 10ln2 - 4,25
Výsledek: 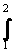 (3x + 2)lnx dx = 10ln2 - 4,25 (3x + 2)lnx dx = 10ln2 - 4,25
|
Aplikace určitého integrálu
Pomocí integrálního počtu je možné vypočítat obsah rovinných útvarů, objemy rotačních těles a délky rovinných křivek.
Velké uplatnění má určitý integrál také ve fyzice a chemii.
Obsah rovinného útvaru
Pokud se jedná o rovinný útvar omezený osou x, přímkami x=a , x=b a grafem spojité, nezáporné funkce y = f(x), pak
je jeho obsah dán určitým integrálem, jak bylo uvedeno u geometrické interpretace
určitého integrálu.

Mějme dánu spojitou a nezápornou funkci f v intervalu <a,b>.Potom udává učitý integrál 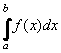 obsah útvaru U (na obrázku) ohraničeného grafem funkce f, osou x a přímkami x = a , x = b.
Tedy: S(U) =
obsah útvaru U (na obrázku) ohraničeného grafem funkce f, osou x a přímkami x = a , x = b.
Tedy: S(U) = 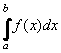
| (51) |
|
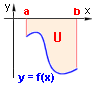 Pokud funkce y = f(x) v intervalu <a,b> nabývá nekladných hodnot, pak vypočteme absolutní hodnotu
příslušného určitého integrálu:
Pokud funkce y = f(x) v intervalu <a,b> nabývá nekladných hodnot, pak vypočteme absolutní hodnotu
příslušného určitého integrálu:
S(U) = |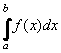 | = - | = - 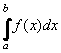
Jestliže funkce y = f(x) nabývá v intervalu <a,b> jak kladných, tak i záporných hodnot, potom tento interval rozdělíme
na dílčí intervaly, ve kterých funkce nabývá pouze nekladných hodnot resp. nezáporných hodnot a vypočteme obsahy podle
předcházejících úvah.
Příklad 65:
Vypočtěte obsah útvaru, který je ohraničen křivkou y = x2 - 1 , osou x
a přímkami x = -2 , x = 3.
| = |
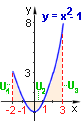 Funkce y = x2 - 1 = (x + 1)(x - 1) protíná osu x v bodech x = -1, x = 1
Funkce y = x2 - 1 = (x + 1)(x - 1) protíná osu x v bodech x = -1, x = 1
a je v intervalech <-2,-1> a <1,3> nezáporná a v intervalu <-1,1> nekladná - viz. obrázek.
Rozdělíme proto interval <-2,3> na tři dílčí intervaly a obsahy dílčích útvarů U1, U2, U3 sečteme.
S(U) = S(U1) + S(U2) + S(U3) =
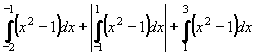 = [x3/3 - x]-1-2 + |[x3/3 - x]1-1| + [x3/3 - x]31 =
-1/3 + 1 - (-8/3 + 2) + |1/3 - 1 - (-1/3 + 1)| + 22/3 - 3 - (1/3 - 1 ) = 28/3 j2 = [x3/3 - x]-1-2 + |[x3/3 - x]1-1| + [x3/3 - x]31 =
-1/3 + 1 - (-8/3 + 2) + |1/3 - 1 - (-1/3 + 1)| + 22/3 - 3 - (1/3 - 1 ) = 28/3 j2
Výsledek: Obsah útvaru je 28/3 j2.
|
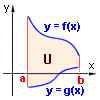
Je-li rovinný útvar ohraničený dvěma křivkami y = f(x) shora a y = g(x) zdola (f, g jsou spojité funkce
a platí g(x)  f(x) - viz obrázek), potom pro jeho obsah platí: f(x) - viz obrázek), potom pro jeho obsah platí:
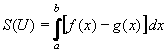 . .
| (52) |
|
Vztah platí i v případě, že některá z funkcí nabývá záporných hodnot (jako je tomu
na obrázku u funkce g).
Jestliže víme, že křivky y = f(x) , y = g(x) se v intervalu (a,b) neprotínají, nemusíme zjišťovat, zda f(x) > g(x) nebo
f(x) < g(x). Vypočteme absolutní hodnotu z inegrálu rozdílu funkcí:
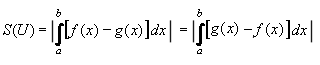
Příklad 66:
Vypočtěte obsah útvaru, který je ohraničen křivkami y = 3 - x2 , y = 2x.
| = |
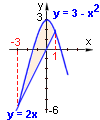 První křivkou je parabola a druhou je přímka - viz obrázek. Abychom určili meze určitého integrálu, musíme zjistit
průsečíky křivek.Řešíme rovnici:
První křivkou je parabola a druhou je přímka - viz obrázek. Abychom určili meze určitého integrálu, musíme zjistit
průsečíky křivek.Řešíme rovnici:
3 - x2 = 2x
x2 + 2x - 3 = 0
x-ové souřadnice průsečíků jsou tedy x= -3 a x = 1. Podle (52) dostáváme:
S(U) = 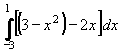 = [3x - x3/3 - x2]1-3 =
3 - 1/3 - 1 - (-9 + 9 - 9) = 11 - 1/3 = 32/3. = [3x - x3/3 - x2]1-3 =
3 - 1/3 - 1 - (-9 + 9 - 9) = 11 - 1/3 = 32/3.
Výsledek: Obsah útvaru je 32/3 j2.
|
Jestliže je útvar omezen třemi a více křivkami, je ho třeba rozložit na několik částí.
Příklad 67:
Vypočtěte obsah útvaru, který je ohraničen křivkami f: y = x2 , g: y = x2/3, h: y = 8 - x2
| = |
Všechny křivky jsou paraboly - viz obrázek. Útvar je souměrný podle osy y. Stačí tedy vypočítat obsah části pro
kladné hodnoty x a vynásobit dvěma. Tuto pravou část musíme rozdělit na dvě části U1 a U2.
Abychom určili meze integrálu, musíme zjistit průsečíky křivek.f, h a g, h. Řešíme rovnici:
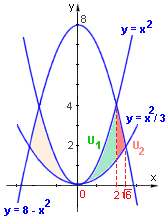 8 - x2 = x2
8 - x2 = x2
x2 = 4
x-ové souřadnice průsečíků f, h jsou tedy x= -2 a x = 2.
8 - x2 = x2/3
x2 = 6
x-ové souřadnice průsečíků g, h jsou tedy x= -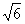 a x = a x = 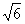 . .
Podle (52) dostáváme:
S(U1) + S(U2) = 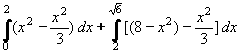 =
[2x3/9]20 + [8x - 4x3/9] =
[2x3/9]20 + [8x - 4x3/9]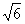 2 =
16/9 + 8. 2 =
16/9 + 8.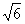 - 8. - 8.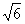 /3 - 16 + 32/9 =
16.( /3 - 16 + 32/9 =
16.(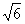 - 2)/3 - 2)/3
Výsledek: Obsah útvaru je 32.(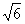 - 2)/3. - 2)/3.
|
Objem rotačního tělesa
 Necháme-li rovinný útvar rotovat kolem osy x, vznikne rotační těleso, jehož objem můžeme vypočítat pomocí
určitého integrálu.
Necháme-li rovinný útvar rotovat kolem osy x, vznikne rotační těleso, jehož objem můžeme vypočítat pomocí
určitého integrálu.
Nechť rotační těleso vznikne rotací křivky y = f(x) kolem osy x (f je nezáporná spojitá funkce) v intervalu <a,b>.
Potom jeho objem V vypočteme podle vztahu:
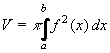
Pokud rotační těleso vznikne rotací křivky x = f(y) kolem osy y (f je nezáporná spojitá funkce) v intervalu <a,b>.
Potom jeho objem V vypočteme podle vztahu:
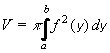
| (53) |
|
Příklad 68:
Odvoďte vzorec pro výpočet objemu rotačního kuželu s poloměrem podstavy r a výškou v.
| = |
Funkce f je přímka určená body [0,0] a [v,r]. Její směrový vektor má souřadnice (v,r) a normálový
vektor (r,-v). Rovnice přímky je tedy rx - vy = 0.
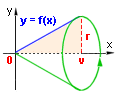 Vyjádříme y: y = rx/v
Vyjádříme y: y = rx/v
Přímku bereme v intervalu <0,v>, to jsou také meze integrálu.
Dosazením do (53) dostáváme:
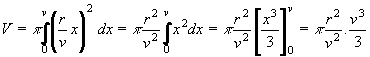 = pr2v/3 j3 = pr2v/3 j3
Výsledek: Objem rotačního kuželu udává vzorec: V = pr2v/3 j3
|
Příklad 69:
Vypočtěte objem rotačního tělesa, které vznikne rotací útvaru ohraničeného křivkami
x2 - y2 = 4, y = -2 , y = 2 kolem osy y.
| = |
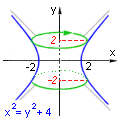 Křivkou omezující rotující útvar je rovnosá hyperbola (a=b=2) pro y z intervalu <-2,2>.
Vznikne rotační těleso znázorněné na obrázku.
Křivkou omezující rotující útvar je rovnosá hyperbola (a=b=2) pro y z intervalu <-2,2>.
Vznikne rotační těleso znázorněné na obrázku.
Z rovnice hyperboly vyjádříme x2: x2 = y2 + 4
a dosadíme do vztahu (53) pro osu y:
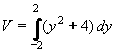 = p(8 + 8/3 + 8 + 8/3) =
= 64p/3 j3 = p(8 + 8/3 + 8 + 8/3) =
= 64p/3 j3
Výsledek: Objem rotačního kuželu je 64p/3 j3
|
A to již konec kurzu Limita , derivace, integrál.
Přehled použité a doporučené literatury:
PhDr.Ivan Bušek - Řešené maturitní úlohy z matematiky, SPN 1988
Petr Benda a kol. - Sbírka maturitních příkladů z matematiky, SPN 1983
RNDr.Dag Hrubý, RNDr.Josef Kubát - Matematika pro gymnázia - Diferenciální a integrální počet, Prometheus 1997
Prof.dr.Beloslav Riečan, DrSc. a kol. - Matematika pro IV.ročník gymnázií, SPN 1987
František Vejsada, František Talafous - Sbírka úloh z matematiky pro gymnázia, SPN 1969
B. Příklady s krokovou kontrolou e-učitele
C. Příklady na procvičení učiva
Na následujících příkladech s výsledky se můžete zdokonalit ve znalostech učiva této lekce.
Pokud si nevíte s příkladem rady, užijte stručné nápovědy - Help.
| Příklady označené | A mají největší obtížnost, | B střední a | C nejmenší. |
D. Kontrolní test
E.Náhodný test
F. Hodnocení výsledků a komunikace s učitelem (tutorem)
Vytisknout certifikat
Hodnocení výsledků:
Komunikace s učitelem (tutorem):
Tato část je určena pouze pro registrované uživatele. Zaregistrujte se!
|

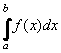 obsah útvaru U (na obrázku) ohraničeného grafem funkce f, osou x a přímkami x = a , x = b.
obsah útvaru U (na obrázku) ohraničeného grafem funkce f, osou x a přímkami x = a , x = b. 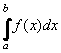 = S(U)
= S(U)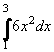
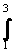 x(1 - x)2dx
x(1 - x)2dx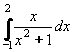
 (3x + 2)lnx dx
(3x + 2)lnx dx
 Pokud funkce y = f(x) v intervalu <a,b> nabývá nekladných hodnot, pak vypočteme absolutní hodnotu
příslušného určitého integrálu:
Pokud funkce y = f(x) v intervalu <a,b> nabývá nekladných hodnot, pak vypočteme absolutní hodnotu
příslušného určitého integrálu: 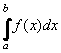 | = -
| = - 
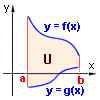
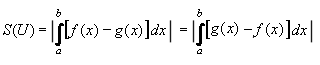
 Necháme-li rovinný útvar rotovat kolem osy x, vznikne rotační těleso, jehož objem můžeme vypočítat pomocí
určitého integrálu.
Necháme-li rovinný útvar rotovat kolem osy x, vznikne rotační těleso, jehož objem můžeme vypočítat pomocí
určitého integrálu.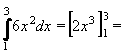 2.33 - 2.13 = 52
2.33 - 2.13 = 52
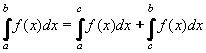
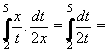
 Funkce y = x2 - 1 = (x + 1)(x - 1) protíná osu x v bodech x = -1, x = 1
Funkce y = x2 - 1 = (x + 1)(x - 1) protíná osu x v bodech x = -1, x = 1 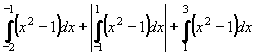 = [x3/3 - x]-1-2 + |[x3/3 - x]1-1| + [x3/3 - x]31 =
-1/3 + 1 - (-8/3 + 2) + |1/3 - 1 - (-1/3 + 1)| + 22/3 - 3 - (1/3 - 1 ) = 28/3 j2
= [x3/3 - x]-1-2 + |[x3/3 - x]1-1| + [x3/3 - x]31 =
-1/3 + 1 - (-8/3 + 2) + |1/3 - 1 - (-1/3 + 1)| + 22/3 - 3 - (1/3 - 1 ) = 28/3 j2 f(x) - viz obrázek), potom pro jeho obsah platí:
f(x) - viz obrázek), potom pro jeho obsah platí: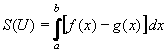 .
.
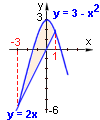 První křivkou je parabola a druhou je přímka - viz obrázek. Abychom určili meze určitého integrálu, musíme zjistit
průsečíky křivek.Řešíme rovnici:
První křivkou je parabola a druhou je přímka - viz obrázek. Abychom určili meze určitého integrálu, musíme zjistit
průsečíky křivek.Řešíme rovnici: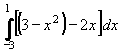 = [3x - x3/3 - x2]1-3 =
3 - 1/3 - 1 - (-9 + 9 - 9) = 11 - 1/3 = 32/3.
= [3x - x3/3 - x2]1-3 =
3 - 1/3 - 1 - (-9 + 9 - 9) = 11 - 1/3 = 32/3.  8 - x2 = x2
8 - x2 = x2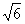 a x =
a x = 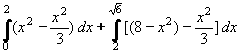 =
[2x3/9]20 + [8x - 4x3/9]
=
[2x3/9]20 + [8x - 4x3/9]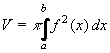
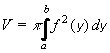
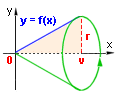 Vyjádříme y: y = rx/v
Vyjádříme y: y = rx/v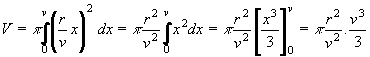 = pr2v/3 j3
= pr2v/3 j3 Křivkou omezující rotující útvar je rovnosá hyperbola (a=b=2) pro y z intervalu <-2,2>.
Vznikne rotační těleso znázorněné na obrázku.
Křivkou omezující rotující útvar je rovnosá hyperbola (a=b=2) pro y z intervalu <-2,2>.
Vznikne rotační těleso znázorněné na obrázku. 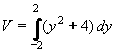 = p(8 + 8/3 + 8 + 8/3) =
= 64p/3 j3
= p(8 + 8/3 + 8 + 8/3) =
= 64p/3 j3