| Matika krokem - 1.lekce ... |
|
Limita, derivace a integrál 1.lekce - Limita funkce a základní metody jejího výpočtu |
Vytisknout |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Skype výuka, doučování
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
A. Výklad a ukázkové příklady
Limita funkce Při výkladu nových pojmů se budeme snažit dodržovat následující postup:  1. Na příkladě přiblížíme význam pojmu 2. Volně, intuitivně naformulujeme. 3. Matematicky upřesníme definici. Začneme tedy příkladem. Zkoumejme chování funkce  v okolí bodu x = 2.Funkce f není v bodě x=2 definována. Blíží-li se však proměnná x k číslu 2, blíží se hodnota y k číslu 4. To je zřejmé z grafu funkce i z následující tabulky:
Číslo 4 nazýváme limitou funkce f v bodě x=2. (latinsky limes znamená hranice) Zapisujeme:  Intuitivně limita představuje hodnotu, k níž se nějaká proměnná veličina neomezeně blíží. Jestliže se při neomezeném přibližování x k a (v našem příkladě a=2) hodnota funkce y=f(x) neomezeně blíží k L (v našem příkladě L=4), pak říkáme, že funkce y=f(x) má v bodě a limitu L a matematicky zapisujeme:  Jak to ale vyjádřit přesněji, matematicky? Skutečnost, že se cosi k nějaké hodnotě neomezeně blíží, můžeme také formulovat tak, že se k této hodnotě blíží libovolně blízko. Tedy lze vždy najít hodnoty proměnné x, pro které jsou odpovídající hodnoty funkce zvoleně blízko k limitě L, popřípadě ještě blíž. Jinak řečeno: K libovolně malé "blízkosti" hodnoty funkce k limitě L lze vždy najít hodnoty proměnné z "blízkosti" čísla a, pro které jsou odpovídající hodnoty funkce k L ještě bližší. "Blízkost" čísel budeme matematicky posuzovat pomocí absolutní hodnoty rozdílu čísel. V našem příkladě zvolíme "blízkost" funkce f k limitě 4 například 0,01 tedy:  (*)a chceme najít hodnoty x, pro které jsou odpovídající hodnoty funkce v "blízkosti" 0,01 k limitě 4, popř. ještě blíž. Jak je dostaneme? Po úpravách vnitřku abs.hodnoty dostáváme: |x - 2|= 0,01 (**). Tvrzení (*) a (**) jsou ekvivalentní, z jednoho plyne druhé a obráceně, proto tedy pro: |x - 2| < 0,01 bude i  .Tedy pro x z "blízkosti" k 2 menší než 0,01 bude hodnota funkce f z ještě menší blízkosti k 4 než 0,01. Obecně označme libovolnou "blízkost" funkce k limitě L symbolem e a budeme ji posuzovat pomocí |f(x) - L| a "blízkost" proměnné x k bodu a označme d a budeme ji posuzovat pomocí |x - a|. Hodnota f(x) je k L v menší "blízkosti" než e zapíšeme matematicky |f(x) - L| < e nebo-li f(x) patří do intervalu (L - e,L + e). Podobně proměnná x je k a v menší "blízkosti" než d zapíšeme matematicky |x - a| < d nebo-li x patří do intervalu (a - d,a + d). 
Nyní již můžeme konečně matematicky definovat pojem limity funkce:
Výpočet limity funkce Každá funkce má zřejmě v daném bodě nejvýše jednu limitu, ale jak se vypočítá? Nejsnáze je možno určit limitu funkcí spojitých.
Příklad 1: Vypočtěte 
Jak ale poznáme, že je funkce spojitá? Snadno to poznáme z grafu. Grafem spojité funkce je plynulá, nepřerušovaná křivka. Graf spojité funkce lze tedy nakreslit jedním tahem. 
Ze znalostí vlastností a grafů elementárních funkcí vyplývají následující tvrzení:
V těchto případech tedy počítáme limitu jako funkční hodnotu: Příklad 2: Vypočtěte  .
Příklad 3: Vypočtěte 
V příkladech se ale často setkáváme s funkcemi, které v bodě a nejsou definovány, a tedy nemohou být v bodě a ani spojité.Potom můžeme využít následující věty o limitě dvou funkcí:
Příklad 4: Vypočtěte 
Věty o limitě dvou funkcí požíváme velmi často při výpočru limit racionálních funkcí. Příklad 5: Vypočtěte 
Některé limity nám umožní vypočítat věta o třech limitách:
Příklad 6: Vypočtěte 
Tuto limitu je třeba si zapamatovat (pro další výpočty) jako základní goniometrickou limitu (třeba) Z1:
Pro limity funkcí dále platí důležitá a zřejmá věta o limitě operací - součtu, rozdílu, součinu a podílu funkcí:
Slovně: Limita součtu, rizdílu, součinu a podílu funkcí je rovna součtu, rozdílu, součinu a podílu (nenulový jmenovatel) limit jednotlivých funkcí. Při výpočtu limit goniometrických funkcí se snažíme využít základní goniometrické limity Z1. Příkla 7: Vypočtěte 
Příkla 8: Vypočtěte 
Obsahují-li funkce odmocniny, často pomůže jejich odstranění a výpočet limity je pak již snadný. Příkla 9: Vypočtěte 
B. Příklady s krokovou kontrolou e-učitele C. Příklady na procvičení učiva Na následujících příkladech s výsledky se můžete zdokonalit ve znalostech učiva této lekce. Pokud si nevíte s příkladem rady, užijte stručné nápovědy - Help.
D. Kontrolní test E.Náhodný test F. Hodnocení výsledků a komunikace s učitelem (tutorem) Komunikace s učitelem (tutorem): Tato část je určena pouze pro registrované uživatele. Zaregistrujte se! |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
) ,
exponenciální a goniometrické funkce jsou spojité v každém bodě svého definičního oboru.
.
a pro funkci h(x) platí: 
(je "sevřena" těmito funkcemi) ,
Z vlastností goniometrických funkcí a z obrázku lze v I.kvadrantu odvodit:
)
je určitě menší než obsah trojúhelníka STA (
) 
z toho dostáváme
.
.
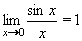
a 
, potom platí:
