A. Výklad a ukázkové příklady
Pan Sörensen zavedl symbol pH, který slouží k přesnému popisu kyselosti roztoku.
Vodné roztoky jsou podle pH: 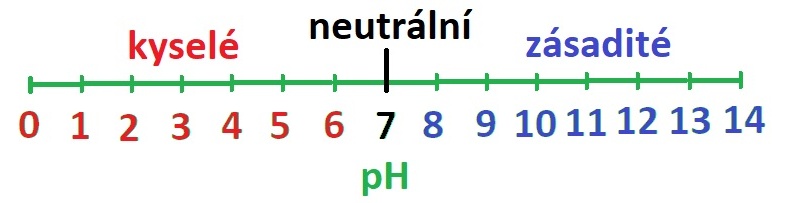
A jsou tím kyselejší, čím je pH menší než 7, tím zásaditější, čím je pH větší než 7.
Kyselina je podle pana Arrhenia látka, která je schopná
odštěpovat kationty H+, zásada odštěpuje anioonty OH-.
V kyselém vodném roztoku tedy převažují kationty H+, naopak v zásaditém převažují anioty OH-.
V neutrálním vodném roztoku je jejich koncentrace stejná a měřením bylo zjištěno, že platí:
[H+] = [OH-] = 10-7.
Pro jejich součin tedy platí:
[H+] . [OH-] = 10-14
Tento vztah platí pro každý vodný roztok a nazývá se iontový součin vody.
Je-li např. v roztoku koncentrace [H+] = 10-2 , je koncentrace [OH-] = 10-12 (
10-2 . 10-12 = 10-14 platí iontový součin vody). Tento roztok bude kyselý,
protože je koncentrace [H+] větší než [OH-] (10-2 > 10-12).
Je-li v jiném roztoku koncentrace [H+] = 10-9 , je koncentrace [OH-] = 10-5 (
10-9 . 10-5 = 10-14 platí iontový součin vody). Tento roztok bude zásaditý,
protože je koncentrace [OH-] větší než [H+] (10-5 > 10-9).
Počítání s mocninami se zápornými exponenty není zrovna příjemné, proto zmíněný pan Sörensen zavedl pojem
pH pomocí definice:
pH = -log [H+]
Tím se zjednodušeně počítá pouze s exponenty mocnin 10 bez záporného znaménka.
První roztok je kyselý, protože má pH = 2 (pH = -log 10-2 = 2), druhý roztok je zásaditý, protože má pH = 9 (pH = -log 10-9 = 9).
Kyselina HA je tím silnější, čím snadněji odštěpuje hydroniové kationty H+, tedy do jaké míry probíhá
její disociace na ionty: HA --> H+ + A-
Tu nám numericky charakterizuje tzv. disociační konstanta kyseliny KHA:
KHA = 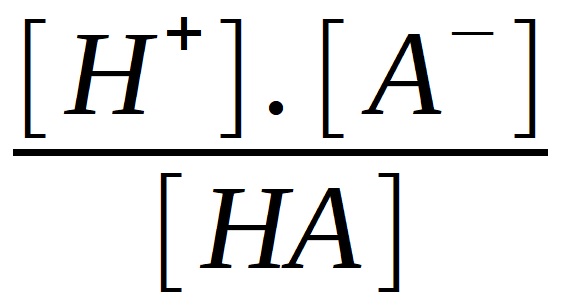
Disociční konstanty jsou pro vodné roztoky u většiny kyselin a zásad dobře známy. Síla kyseliny roste s rostoucí hodnotou
disociační konstanty.
Všechna dosud uvedená fakta (včetně definice pH) však platí jen pro značně zředěné roztoky (menší
než 1M). Se vzrůstající koncentrací roztoků se také zvětšuje vzájemné působení iontů v roztoku a tím klesá jejich "aktivita".
Výpočet pH je pro tyto roztoky pak již nemožný.
Výpočet pH můžeme tedy provádět pouze u velmi zředěných vodných roztoků:
|
(41)
{42)
{43)
|
| |
|
1. Roztoky silných kyselin a silných zásad mají pH určené pouze koncentrací.
Silné kyseliny (HClO4, HCl, H2SO4, HNO3 - nejznámější, seřazeny podle síly, zapamatovat) a silné zásady (NaOH, KOH) jsou ve vodě
praktiocky úplně štěpeny na ionty. Koncentrace hydroniových iontů H+ je rovna koncentraci kyseliny ck a tedy
pH = -log H + = -log ck
pH = -log ck
U zásady je koncentrace hydroxilových iontů OH- rovna koncentraci zásady cz a tedy
pH = - log [H +] = -log 10-14/[OH-] = 14 + logc z
pH = 14 + logc z
|
Příklad1: Jaké pH má roztok 0,1 M HCl?
| = |
Kyselina chlorovodíková je silná kyselina (úplně se štěpí na ionty), je proto koncentrace hydroniových iontů prakticky
rovna koncentraci kyseliny:
[H+] = 0,1 = 10-1
a tedy podle (42) definice pH:
pH = -log [H+] = - log 10-1 = -(-1)= 1
Výsledek: 0,1 M roztok HCl má pH = 1.
|
Příklad 2: Jaké pH má roztok 0,03 M HNO3?
| = |
Kyselina dusičná je silná kyselina (úplně se štěpí na ionty), je proto koncentrace hydroniových iontů prakticky
rovna koncentraci kysliny
[H+] = 0,03 = 3.10-2
a tedy podle (42) definice pH:
pH = -log [H+] = - log 3.10-2 = -(log3 - 2)= -(0,48 - 2) = 1,52
Výsledek: 0,03 M roztok HNO3 má pH = 1,52.
|
Příklad 3: Jaké pH má roztok 0,006 M KOH?
| = |
Hydroxid draselný je silná zásada (úplně se štěpí na ionty), je proto koncentrace hydroxylových iontů prakticky
rovna koncentraci zásady
[OH-] = 0,006 = 6.10-3.
Pomocí iontového součinu vody (41) vypočteme: [H+] = 10-14/(6.10-3) = 6-1.10-11
a tedy podle (42) definice pH:
pH = -log [H+] = - log (6-1.10-11) = -(-log6 - 11)= -(-0,78 - 11) = 11,78
Nebo stručně podle vzorce pH = 14 + logc z = 14 + log 0,006 = 14 + log 6.10-3 = 14 + log6 - 3 =
11 + 0,778 = 11,78
Výsledek: 0,006 M roztok KOH má pH = 11,78.
|
2. U roztoků slabých jednosytných kyselin a slabých zásad
vypočteme pH pomocí disociační konstanty a koncentrace.
Pro disociaci kyseliny HA platí:
HA <--> H+ + A-
Vyjádříme disociační konstantu:
KHA = 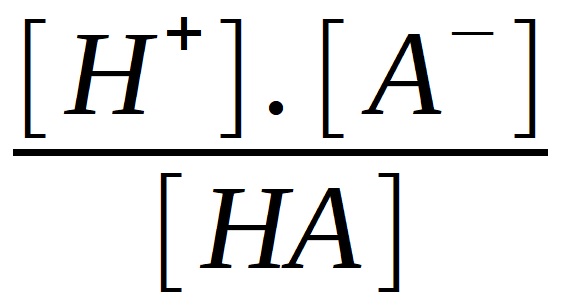
Protože z rovnice disociace plyne, že [H+] = [A-], vztah zjednodušíme:
KHA = 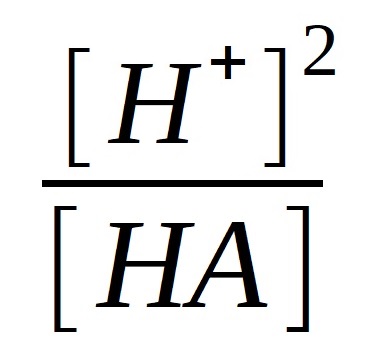
Vyjádříme [H+]:
[H+] = 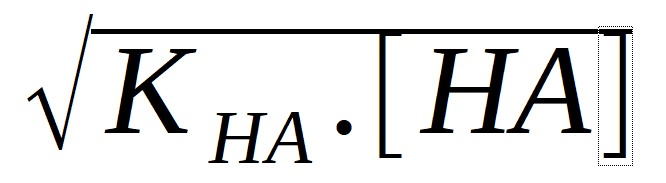
Slabé kyseliny jsou nepatrně disociovány a proto můžeme koncentraci nedisociované kyseliny
položit rovnu koncentraci kyseliny ck, tedy [HA} = ck.
Tím dostáváme:
[H+] = 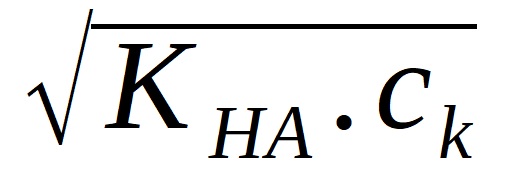
a po zlogaritmování:
log H+ = 1/2(log KHA + log ck)
Nakonec rovnici vynásobíme (-1):
-log H+ = 1/2(-log KHA - log ck).
a dosadíme z definice pH za -log H + = pH
Podobně jako pH se definuje také pK:
pKHA = -log KHA
a dosadíme za -log KHA = pKHA = pKk, (k označuje kyselinu HA - pro stručnost) a máme výsledný vztah pro
výpočet pH slabé jednosytné kyseliny:
pH = 1/2(pKk - log ck)
Podobně, ale stručněji, odvodíme vztah pro slabou, jednosytnou zásadu BOH:
BOH <--> B+ + OH-
KBOH = 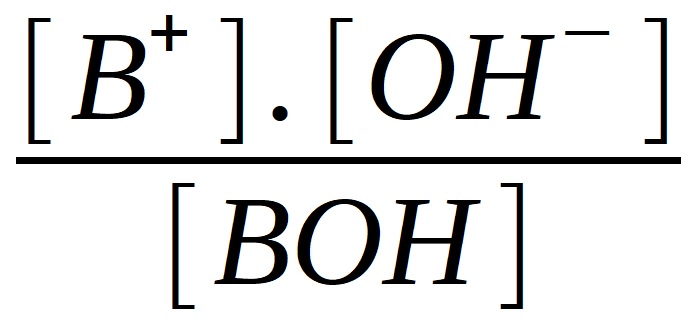
KBOH = 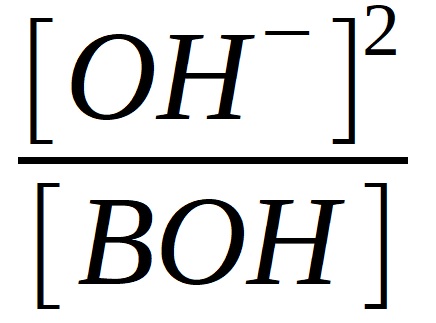 , platí [BOH] = cz , platí [BOH] = cz
[OH-] = 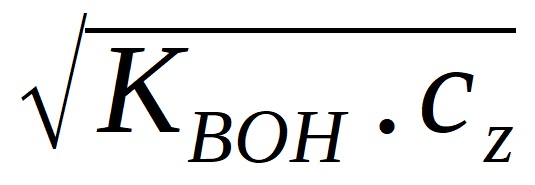
[H+] = 10-14/ 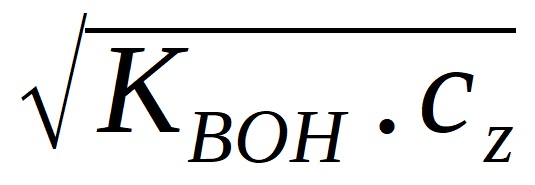
log H+ = -14 - 1/2(log KBOH + log cz)
-log H+ = 14 - 1/2(-log KBOH - log cz)
dosadíme za -log KBOH = pKBOH = pKz, (z označuje zásadu BOH - pro stručnost) a máme výsledný vztah pro
výpočet pH slabé jednosytné zásady:
pH = 14 - 1/2(pKz - log cz)
|
(44)
(45)
(46) |
|
Příklad 4: Jaké pH má roztok 0,1N kyseliny mravenčí HCOOH, je-li její disociační konstanta
Kk = 1,8.10-4.
| = |
Kyselina mravenčí patří mezi slabé kyseliny a proto použijeme pro výpočet pH vztahu (45)
pH = 1/2(pKk - log ck).
Nejprve podle vztahu (44) vypočteme pKk = -logKk = -log 1,8.10-4 = -(log 1,8 + log 10-4 = -(0,255 - 4) = 4,255.
Potom dosadíme:
pH = 1/2(pKk - log ck) = 1/2(4,255 - log 0,1) = 1/2(4,255 - log 10-1) = 1/2(4,255 + 1) = 2,63.
Výsledek: 0,1 M roztok HCOOH má pH = 2,63.
|
Příklad 5: Jaké pH má roztok 0,1N amoniaku, je-li jeho disociační konstanta
Kz = 1,8.10-5.
| = |
Amoniak (hydroxid amonný) patří mezi slabé zásady a proto použijeme pro výpočet pH vztahu (46)
pH = 14 - 1/2(pKz - log cz).
Nejprve podle vztahu (44) vypočteme pKz = -logKz = -log 1,8.10-5 = -(log 1,8 + log 10-5 = -(0,255 - 5) = 4,745.
Potom dosadíme:
pH = 14 - 1/2(pKz - log cz) = 14 - 1/2(4,745 - log 0,1) = 14 - 1/2(4,745 - log 10-1) = 14 - 1/2(4,745 + 1) = 14 - 2,87 = 11,13.
Výsledek: 0,1 M roztok amoniaku má pH = 11,13.
|
B. Příklady s krokovou kontrolou e-učitele
C. Příklady na procvičení učiva
Na následujících příkladech s výsledky se můžete zdokonalit ve znalostech učiva této lekce.
Pokud si nevíte s příkladem rady, užijte stručné nápovědy - Help.
| Příklady označené | A mají největší obtížnost, | B střední a | C nejmenší. |
D. Kontrolní test
E. Hodnocení výsledků a komunikace s učitelem (tutorem)
Vytisknout certifikat
Hodnocení výsledků:
Komunikace s učitelem (tutorem):
Tato část je určena pouze pro registrované uživatele. Zaregistrujte se!
|
